________________________________________________________

Combinaison de classifieurs dans le cas de classes déséquilibrées : application à la prévision du risque cardio-vasculaire

________________________________________________________

Alexandre Pitti

DEA IARFA

Université Pierre et Marie Curie

Rapport de stage de DEA IARFA

réalisé au LIP6 sous la direction de

Florence d’Alché Buc et Christophe Marsala

avril à septembre 2002

Résumé.

Dans de nombreux domaines, l’acquisition massive de données est dorénavant possible, mais le traitement de ces données est trop souvent confronté au bruit et à la redondance de l’information. Dans les problèmes de diagnostic, un fort déséquilibre peut apparaître entre les classes qui empêche les algorithmes classiques d’apprendre les données minoritaires. L’étude de ce problème depuis quelques années a donné naissance à plusieurs stratégies et à l’élaboration de divers classifieurs avec plus ou moins de succès. Notre travail de stage a consisté à aborder ce problème par le biais des données réelles du projet INDANA qui porte sur la prévision du risque cardio-vasculaire. Nous présentons différentes extensions algorithmiques dans le cadre des méthodes de combinaison telles que le « bagging » et le « boosting ». Trois nouveaux algorithmes de classification, BalancedBagging, Cost-Sensitive MarginBoost et ClusteredSampling sont proposés et étudiés empiriquement sur les données réelles.

I Introduction.

En dépit d’une baisse importante depuis 10 ans, les maladies cardiaques restent une cause majeure de mortalité évitable avant 65 ans, et sont parmi les premières causes d’incapacité et de décès après 65 ans. Le contrôle plus efficace des facteurs de risque cardio-vasculaires est un enjeu d’actualité. Aujourd’hui, une approche diagnostique basée sur l’estimation du risque s’avère plus pertinente que l’approche traditionnelle fondée sur le diagnostic de facteurs de risque (hypertension artérielle, hypercholestérolémie, etc.) pour la réduction du risque de maladies cardio-vasculaires. En effet, la prédiction du risque permet d’identifier les sujets qui bénéficieront le plus du traitement avec une sensibilité et une spécificité plus grandes que la mesure de la pression artérielle. Le projet, INDANA, s’inscrit dans le cadre de cet objectif. Il réunit les données individuelles de 10 essais thérapeutiques mises en forme par l’Unité de Pharmacologie Clinique de L’Université de Lyon 1 (la description de la base INDANA est présentée en annexe). Le but de ce stage de DEA, dans le cadre de ce projet, est de proposer et d’évaluer différentes méthodes de combinaison de classifieurs afin d’y parvenir.

II Position du problème.

Nous posons le problème de prédiction du risque cardio-vasculaire comme un problème d’apprentissage supervisé à partir de données, dont l’événement à prédire est représenté par deux classes (événement survenu ou non survenu).

Des analyses des données INDANA ont conduit à identifier des problèmes spécifiques autour de l’existence d’une zone intermédiaire de risque dans laquelle les modèles de prédiction existant reste peu performants [3], [7] et [25]. En effet, les données ne permettent pas une séparation idéale entre exemples positifs et négatifs. La frontière entre positifs et négatifs forme une « zone grise » où les exemples des deux classes s’entremêlent.

De plus, la faible prévalence de l’événement à prédire (la proportion de décès dans la base d’apprentissage est de l’ordre de 6%) constitue un obstacle à l’apprentissage d’une classification binaire car la majorité écrasante d’exemples négatifs a tendance à être « privilégiée » par la majorité des algorithmes existants. Il s’agit donc ici de se confronter à un problème de distribution des exemples positifs et négatifs.

Dans un premier temps nous commençons par expliquer pourquoi les algorithmes qui visent à optimiser le taux de classification faillent et quelles ont étés les approches prises par la communauté scientifique face à ce problème. Ensuite nous expliquons pourquoi ces approches ne peuvent être utilisées telles quelles pour ce projet. Enfin nous présentons trois nouvelles stratégies que nous avons mises en œuvre spécifiquement : BalancedBagging, Cost-Sensitive MarginBoost et ClusteredSampling.

III Etat de l’art.

1 Problème d’apprentissage des classifieurs classiques lorsque les classes ne sont pas équilibrées.

Les classifieurs bayésiens sont construits de telle sorte que la frontière de décision optimale soit celle qui minimise la probabilité d’erreur en prédiction. Une instanceest ainsi associée à la classe la plus vraisemblable ayant la probabilité a posteriori la plus grande. Or cette inégalité ne peut être facilement satisfaite lorsque les classes sont déséquilibrées car (cf. [1] & [13]).

Tous les classifieurs qui visent à optimiser un coût symétrique (taux d’erreurs) se comportent de la même manière. Prenons l’exemple des arbres de décision. N’importe quelle dichotomie peut être représentée avec un arbre, mais après élagage une politique est d’associer à une branche la classe ayant la majorité d’instances. Si les données sont bruitées, certaines régions propres aux deux classes se verront étiquetées de la classe majoritaire. Le manque d’instances d’une classe ne permet pas de délimiter correctement la surface de décision de celle-ci.

Weiss et Provost [28] ont étudié l’effet de la distribution d’une classe sur les performances en apprentissage des arbres de décision : la figure suivante montre quatre courbes ROC, chacune provenant du même jeu de données mais avec une distribution différente.

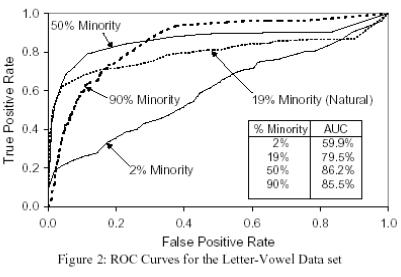
Les résultats montrent la sensibilité des arbres de décision sur l’apprentissage de différentes distributions d’une classe. La meilleure performance est obtenue lorsque les classes sont équilibrées (la classe minoritaire à 50%), la moins bonne lorsque la classe minoritaire ne représente que 2% de la distribution.

Deux stratégies a priori différentes ont été proposées par la communauté scientifique pour résoudre ce problème.

2 Stratégies mises en jeu.

La première stratégie est de rééquilibrer la distribution des données de telle sorte qu’elles deviennent équiprobables (où les classifieurs se comportent le mieux). Ce sont les méthodes de sur-échantillonnage de la classe minoritaire ou de sous-échantillonnage des classes majoritaires [15] et [16].

La seconde est de reformuler le problème d’optimisation : il ne s’agit plus pour un classifieur de minimiser le taux d’erreur où toutes les erreurs ont le même coût, mais de minimiser un taux d’erreur « rééquilibré » en associant à chaque erreur un coût dépendant de la classe de l’instance. Ce taux d’erreur est donc conditionnel aux classes prédites. Les mauvaises classifications faites n’ont plus alors le même coût. Une mauvaise prédiction d’une instance de la classe minoritaire aura ainsi plus d’importance qu’une mauvaise prédiction d’une instance de la classe majoritaire. Ce type d’algorithmes comprend les algorithmes sensibles au coût d’erreur, développés spécifiquement, et ceux qui modifient les prédictions des classifieurs standards (qui minimisent le taux d’erreurs) pour les rendre sensible au coût d’erreur.

D’autres techniques ont été présentées comme la pondération des exemples d’apprentissage par Pazzani [20], l’utilisation du Bootstrap par Catlett [4] et par Sung et Poggio [24], l’échantillonnage hétérogène de Lewis et Catlett [19] et l’observation de relations spécifiques entre certains attributs par Ezawa [10] en accord avec les principes des deux stratégies énoncées précédemment.

3 Méthodes de rééquilibrage des données.

Les méthodes d’échantillonnage modifient la distribution des classes de la base d’apprentissage. Elles peuvent être de deux types : l’ajout d’instances des classes minoritaires ou le sous-échantillonnage des classes majoritaires. Ces approches ne sont pas équivalentes en terme de performance d’apprentissage et de prédiction.

1) L’ajout d’instances.

L’ajout d’instances consiste à augmenter le nombre d’instances de la classe minoritaire en générant des points additionnels à partir de points existants, par interpolation (à l’intérieur du domaine de définition) ou extrapolation (à l’extérieur du domaine de définition).

Si les probabilités a priori des classes se rééquilibrent, cette méthode a cependant des inconvénients : outre le temps d’apprentissage qui augmente, un phénomène de sur-apprentissage peut apparaître. La zone de décision trouvée alors ne correspond pas nécessairement à la véritable (qui reste inconnue) et est biaisée par les valeurs d’instances redondantes. La variance, et donc la probabilité a priori de régions inconnues existantes de la classe, serait plus faible. Le critère de meilleur taux de classification n’est donc pas totalement pertinent, toutefois en augmentant légèrement le nombre d’instances vers un équilibre des distributions, les performances tendent à s’améliorer.

2) Le sous-échantillonnage.

Le sous-échantillonnage consiste à éliminer des instances de la classe majoritaire (sélection des instances les plus représentatives). Cette technique a été utilisée entre autres par Kubat et Matwin [16] dans le but d’obtenir une base d’apprentissage plus équilibrée qui puisse diminuer les inconvénients évoqués des classifieurs. Ils se sont employés à supprimer les exemples à la frontière de décision, ceux bruités qui ne font que complexifier le problème et ceux redondants qui ne font qu’augmenter la probabilité a priori de la classe majoritaire.

Le sous-échantillonnage est une méthode efficace mais qui n’a pas de mesures de contrôle sur les performances. Intuitivement, le taux de classification des instances minoritaires est maximisé  pour un sous-échantillonnage qui équilibre les distributions des classes et diminue la complexité. Chawla [5] propose quant à lui de combiner les deux types d’échantillonnage.

Pourtant, Elkan [8] montre qu’il n’est pas nécessaire de modifier la base d’apprentissage mais qu’il faut plutôt calculer les décisions optimales selon un coût d’erreur attribué à chaque classe. Ceci introduit la seconde voie étudiée par la communauté scientifique : les algorithmes sensibles aux coûts d’erreur.

4 Méthodes de rééquilibrage des coûts d’erreur.

Ces classifieurs ont été proposés pour prendre en compte les erreurs de classification qui n’ont pas les mêmes coûts selon la classe (cf. [1] et [13]).

Le principe de base de la décision sensible aux coûts est le suivant : il peut être intéressant de considérer qu’une instance appartienne à une classe même si d’autres classes sont plus probables.

Une matrice modélise les coûts de mauvaises prédictions pour un problème à deux classes.

	Vraie classe 0	Vraie classe 1
Prédiction classe 0
Prédiction classe 1

Le coût d’étiquetage d’une instance de la classe comme étant de classe vaut donc.

Pour pénaliser les erreurs, il faudra donc vérifier et. Dans notre cas, on pénalisera plus une erreur de prédiction faite sur une instance de la classe minoritaire que l’inverse. Si la classe 1 représente la classe minoritaire alors il faut vérifier aussi.

La prédiction optimale pour une instance sera maintenant la classe qui minimise  le coût d’erreur de prédiction pondéré par la probabilité a posteriori. Cette mesure est appelée le risque [1].

D’où ( : une instance, : classe)

La nouvelle frontière de décision pour un problème à deux classes est la limite où le risque d’erreur est égal. Soit.

Donc lorsque

Différentes manières ont été proposées pour rendre sensible aux coûts les classifieurs classiques. Les principales sont MetaCost de Domingos [7], AdaCost de Fan, Stolfo, Chan et Zhan [3], CSB de Ting [25] et Direct Cost-Sensitive Decision-Making de Zadrozny et Elkan [9].

Ces algorithmes ont le désavantage de n’avoir été testés que sur des bases sans commune mesure avec le déséquilibre de la base INDANA. Leurs assez faibles performances sur celle-ci (cf. annexe) nous ont conduit à vouloir adapter les idées des méthodes de rééquilibrage de données et de coût d’erreur. Ainsi nous présentons dans la partie suivante trois nouveaux types de classifieurs conçus spécifiquement pour le projet INDANA que nous avons nommés BalancedBagging, Cost-Sensitive MarginBoost et ClusteredSampling.

IV Combinaison de classifieurs.

Le succès du Bagging [2] ou du Boosting [11] a montré qu’il était possible dans le cadre des méthodes de combinaison de classifieurs d’obtenir une diminution du biais et de la variance des algorithmes. C’est dans cette perspective que nous avons développés de nouveaux types de combinaison de classifieurs pour le problème plus spécifique du déséquilibre entre classes.

1 BalancedBagging.

Cette méthode est en accord avec les travaux [15, 16, 17, 21, 28] sur l’impact des proportions des distributions sur l’apprentissage des classifieurs. Elle se base sur le principe d’échantillonnage d’instances. Une ébauche de cette idée avait déjà été utilisée dans une forme plus brute par Japkowicz [15].

1) Principe.

Le principe ici est de faire du Bagging [2] « rééquilibré ». A l’origine, dans l’apprentissage par la méthode du Bagging, plusieurs classifieurs apprennent sur des bases obtenues en sélectionnant aléatoirement des instances à partir de la base de données initiale et sont ensuite agrégés pour former une assemblée d’experts. De ce fait, si l’on utilise cette technique en l’état, les bases d’apprentissage auront la même distribution que la base initiale et donc le même déséquilibre.

Le principe du Balanced Bagging est de prendre une probabilité de sélection des instances différente selon leurs appartenances aux classes. Pour surexposer les instances de la classe minoritaire, nous leur attribuons une probabilité d’apparition plus importante que celles de la classe majoritaire. Ainsi un rééquilibrage des distributions est réalisé, grâce auxquelles des bases d’apprentissage sont générées sur lesquelles les algorithmes classiques peuvent alors s’appliquer.

2) Critiques.

Cet algorithme possède les qualités du bagging, à savoir la robustesse face au bruit (un gain sur l’espérance). Ceci est dû au nombre de classifieurs présents qui permettent une meilleure généralisation.

Malheureusement, le Balanced Bagging possède aussi les qualités de ses défauts : l’apprentissage est statique. La modification sur les proportions, une fois fixée avant l’apprentissage, ne permet pas une adaptabilité de l’algorithme comme dans le cas du boosting (apprentissage itératif en fonction des erreurs sur les instances). De plus, le nouveau rapport de rééquilibrage fixé entre les classes n’est qu’un juste compromis global des déséquilibres locaux. Dans certaines régions de l’espace d’entrée, localement, la proportion des classes peut varier ostensiblement par rapport à certaines autres. Le rapport choisi n’est donc qu’un compromis qui n’est optimal que globalement.

2 Cost-Sensitive MarginBoost.

Le « cost-sensitive boosting » a été étudié pour améliorer les performances du boosting surtout dans le cas de problèmes à deux classes. Plusieurs variantes ont été proposées mais seulement sur des bases standards (aucun équivalent en terme de déséquilibre à la base INDANA) : AdaCost de Chan et Stolfo [3], CSB de Ting [25]. Ces algorithmes ont malheureusement de faibles performances sur celle-ci (cf. annexe).

La technique du Boosting [11] permet de créer un algorithme robuste à partir d’une combinaison de faibles classifieurs. Les classifieurs sont agrégés itérativement en minimisant à chaque étape du processus les erreurs sur les instances mal apprises.

Nous avons voulu utiliser l’algorithme de boosting MarginBoost dans ce cadre. MarginBoost est un algorithme de boosting basé sur la minimisation d’un coût inversement proportionnel à la marge d’erreur par descente de gradient. Ainsi, nous étendons la fonction d’erreur sur la marge au coût d’erreur via une matrice des coûts. Il est généralisé au principe du calcul du risque d’erreur afin d’influencer l’apprentissage des instances de la classe minoritaire (cf. Algorithmes sensibles aux coûts d’erreur).

1) Principe.

Rendre un classifieur de base sensible aux coûts passe par l’introduction d’une matrice qui rend compte des préférences que l’on a de certaines instances sur d’autres (cf. état de l’art).

La prédiction de l’algorithme MarginBoost pour la classe j est calculée pour une instance par la combinaison de classifieurs tel que :

,

La classe la plus probable prédite étant

MarginBoost se base sur la minimisation de la fonction de coût définie pour toute fonction décroissante c dépendante de la marge. Afin de rendre l’algorithme sensible au risque d’erreur, les classifieurs entraînés doivent prédire le risque selon la matrice des coûts à chaque étape. Ainsi :

Avec

Et

Il s’agit de trouver un ensemble de classifieurs qui minimise J de manière itérative. L’ajout d’un nouveau classifieur doit être choisit de façon à réduire le gradient d’erreur J.

La convergence de MarginBoost est garantie en minimisant la fonction :

Nous donnons un poidsà chaque instance à l’étape  :

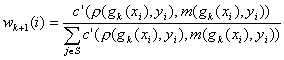
2) Critiques.

Marginboost est un algorithme de boosting. Il pondère après chaque itération le coût d’erreur pour chaque instance. Sa modification afin qu’il puisse pondérer davantage les instances de la classe minoritaire le rend instable. Il peut avoir tendance à surapprendre les instances de la classe minoritaire. Ce défaut propre au boosting fait que MarginBoost ne devrait être utilisé qu’en classification seulement.

3 ClusteredSampling.

Le Balanced Bagging fait un tirage aléatoire des instances avec remise, fois pour la classe majoritaire et fois pour la classe minoritaire. MarginBoost pondère d’une seule façon les instances mal classées via une matrice des coûts selon leurs classes. La classification génère pour ces deux algorithmes des règles heuristiques biaisées du fait de l’échantillonnage aléatoire des instances pour la base d’apprentissage. Un regroupement harmonieux des instances (avec la même proportion et surtout proches spatialement) de chaque classe de l’espace d’entrée pour la base d’apprentissage peut permettre au classifieur d’apprendre une règle très fine (locale) et pertinente sur cet espace. La contrepartie en est sa totale « myopie » sur l’espace dual.

C’est dans cette optique là que l’idée d’une assemblée de classifieurs qui se partageraient ainsi tout l’espace (ou juste la frontière de décision) de manière précise a donné lieu à l’algorithme ClusteredSampling. BalancedBagging et MarginBoost pondèrent les coûts d’erreur de façon à diminuer les différences de performances interclasses. Comme le déséquilibre interclasse est la moyenne des déséquilibres locaux intraclasses, ces deux algorithmes reviennent à donner un coût d’erreur fixe entre les classes. Contrairement à eux, ClusteredSampling revient à faire un algorithme sensible aux coûts d’erreur variables.

Durant ce stage, un algorithme semblable au ClusteredSampling a été proposé par A. Nugroho, S. Kuroyanagi et A. Iwata, [17].

1) Principe.

Regrouper des individus ayant des profils proches permet d’apprendre des règles intraclasses et interclasses plus exploitables sémantiquement. Ces règles mettent en lumière dans un groupe la prévalence d’un ou de plusieurs paramètres sur d’autres pour la prédiction.

L’espace d’entrée est subdivisé en plusieurs groupes (l’assignation d’une instance à un groupe est faite par une distance) sur lesquels des classifieurs apprennent des règles sur chacun eux. La prédiction de la classe pour une instance donnée se fait désormais par le vote des classifieurs des groupes de l’espace d’entrée les plus proches de l’instance. Ainsi le poids du vote d’un classifieur n’est plus fonction seulement de sa marge de confiance mais aussi fonction de sa pertinence synthétisée par la distance entre la région de l’espace apprise et la position de l’instance. Il n’est donc plus utile de prendre en compte les décisions de chaque classifieur, mais seulement celles d’une partie d’entre eux qui seraient les plus fiables.

2) Critiques.

Plus il y a de groupes, plus les instances de chacun d’eux sont proches sémantiquement et plus les règles construites sur chaque groupe sont précises. Mais générer des règles locales est capable d’entraîner un apprentissage instable si la base est complexe. Ces règles peuvent mettre en valeur l’importance d’un paramètre dans un contexte particulier (une région de l’espace) mais peuvent aussi être biaisées à cause du bruit. En outre, cet algorithme est sensible au bruit et il convient d’être critique devant les heuristiques trouvées.

4 Méta-classifieurs.

Ces trois classifieurs : MarginBoost, BalancedBagging et ClusteredSampling apprennent de manière différente l’espace d’entrée. Pris isolément, leurs performances varient selon le type d’instances présentées (cf. Expérimentation, analyse des erreurs des classifieurs), mais la combinaison de ces algorithmes par méta-classifieurs peut améliorer les décisions prises.

En effet, comme dans la réalité, par exemple, l’avis d’un médecin généraliste ou d’un spécialiste n’a pas la même importance selon la pathologie du patient. Via un coordinateur, il est possible d’apprendre les compétences de chacun pour savoir dans quelle mesure faire confiance à l’un, à l’autre, aux deux, voire à aucuns des deux (s’ils n’ont pas les compétences nécessaires devant certains symptômes).

C’est le principe des classifieurs de classifieurs (méta-classifieurs) ou des arbres de classifieurs si le classifieur est un arbre de décisions [13]. Les assemblées de classifieurs à structure dynamique utilisent le signal d’entrée (les attributs du patient) dans un processus d’intégration des sorties des experts en une sortie globale. Les réponses des experts sont non linéairement combinées par un tiers expert appelé routeur.

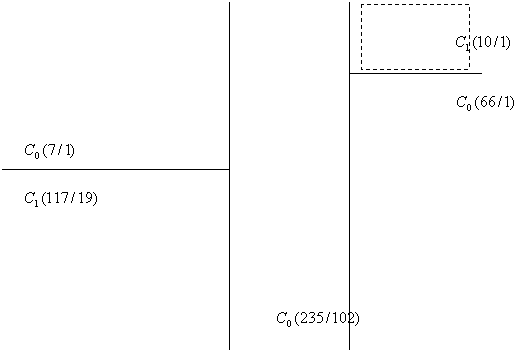
L’apprentissage via un routeur des intervalles de confiance des classifieurs donne une décision plus pertinente que celle de chaque agent pris séparément : regardons un exemple de règles générées par un routeur type arbre de décision (cf. figure 6) :

classifieur1 <= 0.42969

| classifieur2 <= 0.46886: 1 (117.0/19.0)

C1 > 0.67

C2 < 0.46

| classifieur2 > 0.46886: 0 (7.0/1.0)

classifieur1 > 0.42969

C2 > 0.66

| classifieur1 <= 0.67799: 0 (235.0/102.0)

| classifieur1 > 0.67799

C2 < 0.66

| | classifieur2 <= 0.66657: 0 (66.0/1.0)

| | classifieur2 > 0.66657: 1 (10.0/1.0)

Le routeur s’appuie parfois sur la prédiction d’un des deux classifieurs, parfois aux deux suivant le degré de confiance qu’ils ont en leur réponse, mais il est intéressant de noter qu’il peut aussi s’abstraire des certitudes de ceux-ci dans certains cas. Lorsque le classifieur 1 et le classifieur 2 ont tous deux un taux de prédiction supérieur à 0,67 en la classe 0, le routeur établit comme stratégie d’ignorer leurs choix.

1) Principe.

Du fait du problème de la complexité de la base INDANA (existence de la « zone grise », cf. position du problème), il a paru intéressant de ne pas prendre en compte directement pour l’apprentissage du routeur les paramètres des instances (qui restent fortement bruités) mais la sortie des classifieurs qui ont appris sur celles-ci. Cette source indirecte, qui est déjà un traitement des instances, donne une information de plus haut niveau plus riche et stable (du fait de la généralisation des classifieurs). Pour que le routeur ne surapprenne pas les bornes d’apprentissage des classifieurs, une étape de validation croisée est ajoutée dans l’algorithme.

2) Critiques.

Cette nouvelle source d’information que sont les prédictions des classifieurs se trouve être plus intéressante pour l’apprentissage du routeur. En effet, celui-ci apprend les domaines de confiance des classifieurs plutôt que l’espace d’entrée qu’ils ont appris. Il corrige leurs prédictions en décidant du degré de confiance à accorder à chacun et s’octroie ainsi la décision finale. En outre la performance de l’algorithme dépend donc fortement de celle du routeur.

Le nombre de sources est particulièrement important pour l’apprentissage du routeur. Les sources doivent être décorelées le plus possible les unes des autres ce qui implique implicitement que chacune doivent appartenir à des familles de classifieurs différentes. De plus le déséquilibre des classes de la base INDANA présume aussi que le routeur doit « rééquilibrer » les distributions des classes. Le choix du routeur doit donc se faire parmi les classifieurs déjà présentés.

V Expérimentations.

La description de la base INDANA ainsi que les tableaux de résultats des expériences sont donnés en annexe.

Tous les algorithmes présentés ont été développés en Java sous la plateforme GNU Wecka. Tous les résultats obtenus en apprentissage supervisé l’ont été par la méthode de la validation croisée en 10 ensembles, qui consiste à diviser la base d’exemples en plusieurs parties, chaque partie devenant à son tour base d’apprentissage et base de test.

Avant de présenter les résultats des expériences sur les algorithmes proposés, nous montrons d’abord ceux des algorithmes existants spécifiques au problème de déséquilibre des distributions : MetaCost [7], AdaCost [3] et CSB [25]. Ces résultats sur la base INDANA représentent une mesure étalon des performances à comparer avec celles des nouveaux algorithmes.

Il faut noter que la mesure de la précision n’est pas fiable dans ce problème. En effet comme il y a toujours un nombre trop important d’instances pour une classe, cette mesure qui en dépend est biaisée (mesure interclasse). Contrairement au rappel qui est une mesure intraclasse. Il faudrait soit présenter un nombre égal d’instances des 2 classes en test, mais alors les résultats seraient biaisés par la sélection elle-même, soit pondérer une classe par rapport à l’autre.

1 Algorithmes existants.

1) MetaCost.

Les performances de cet algorithme montrent la complexité de la base d’apprentissage. De plus, son principe de réétiquetage d’instance suivant le coût d’erreur le rend instable et difficile à calibrer finement (cf. tableau 1).

2) AdaCost.

L’algorithme de Boosting AdaCost se comporte mieux que MetaCost sur cette base (cf. tableau 2). Ses résultats sont à comparer avec les deux autres algorithmes de Boosting sensibles aux coûts d’erreur que sont CSB et « Cost-Sensitive MarginBoost » qui pondèrent suivant la marge d’erreur (et non plus suivant l’erreur moyenne).

3) CSB.

Comme les autres algorithmes de Boosting, CSB reste très sensible au bruit dans la base. Si sa fonction de pondération des instances est plus pertinente que celle d’AdaCost, elle semble de ne pas être adéquat pour cette base (cf. tableau 3).

2 Nouveaux algorithmes.

1) BalancedBagging.

Cet algorithme obtient de meilleures performances que les algorithmes existant étudiés pour le déséquilibre des classes. Il généralise mieux pour un rapport entre les classes de l’ordre de 0,775 (un quart d’instances de la classe majoritaire en moins que celle minoritaire). Ce rapport est différent de celui attendu par la théorie à savoir 1 (cf. état de l’art sur l’apprentissage avec déséquilibre des classes). Ceci montre soit que les exemples de la classe majoritaire sont redondants, soit que les instances de la classe minoritaire sont moins homogènes (erreur d’étiquetage, plusieurs groupes de personnes…) et donc plus difficiles à apprendre.

Le classifieur SMO obtient de meilleurs résultats que les arbres de décision (cf. tableau 4&5). Comme cet algorithme construit la frontière de décision en fonction des instances de chaque classe, il a besoin d’autant d’instances de chaque classe. C’est pour cela que le rapport entre les 2 classes est plus proche de 1 que pour les arbres de décision.

Remarquons l’influence qu’a le nombre de classifieurs sur l’apprentissage. L’amélioration du biais qui en découle est l’une des propriétés du Bagging. Empiriquement, elle semble avoir été conservée par le BalancedBagging.

L’étude des marges d’erreurs faites par BalancedBagging (cf. tableau 6) sur les instances de la base de test montre que pour 211 cas (10% de la base totale) la classification est aberrante : le taux de prédiction pour une classe est incluse entre [50% - 60%]. Cette information renseigne sur la gravité du risque cardio-vasculaire chez le patient. Ainsi par exemple, il y a 14 profils étiquetés NO_EVENT classés par l’algorithme comme étant critiques (prédiction en la classe EVENT supérieur à 99%). Mais aussi, plus inquiétant, 4 cas étiquetés EVENT diagnostiqués comme étant bien portant (prédiction en la classe NO_EVENT supérieur à 80%). Soit nous n’avons pas assez d’informations sur ces cas (nature extrêmement rare de l’évènement) soit leurs décès sont dus à une autre cause. L’étude de ces cas suspects par des médecins est présentée au paragraphe étude des erreurs de classification.

2) Cost-Sensitive MarginBoost.

Les performances de MarginBoost dépassent celles des autres algorithmes de Boosting, AdaCost et CSB malgré le bruit dans les données (cf. tableau 8).

La version de MarginBoost avec le classifieur SMO est plus stable que celle avec les arbres de décision : l’erreur de classification sur la classe 1 semble proportionnel au coût d’erreur. Les résultats sont à comparer avec ceux du BalancedBagging. MarginCost obtient des performances équivalentes au BalancedBagging aussi bien dans sa version  rééchantillonnage que dans celle de pondération, ce qui montre le bien-fondé de ces deux méthodes.

Mais si les performances se valent, il est intéressant de voir que ces deux classifieurs n’apprennent pas de la même manière (cf. figure 4). La marge de confiance que MarginBoost associe à la prédiction prend des valeurs discrètes. Ce qui implique un manque d’information que l’on peut faire sur la gravité du risque cardio-vasculaire.

Les marges d’erreurs faites par cet algorithme (cf. tableau 9) montre son principal défaut comparativement à BalancedBagging. La forte pondération de certaines instances de la base entraîne un sur-apprentissage qui biaise sa valeur de prédiction. Ceci fait qu’il ne peut être utilisé en diagnostic mais seulement en pronostic et que la réponse qu’il peut donner est instable.

La limite en généralisation semble être atteinte par les deux classifieurs. Après avoir amélioré les performances sur le problème de distribution des classes, nous nous confrontons à présent à celui de la complexité de la base. Ce second problème évoqué dans l’introduction est celui de la « zone grise ». Nous essayons dans cette seconde partie d’étudier plus en détails les caractéristiques de la base INDANA ainsi que les erreurs faites par les classifieurs afin de comprendre ce qui se passe et si des améliorations sont possibles.

3) ClusteredSampling.

Il est normal que les résultats de ce classifieur (cf. tableau 10)  soient moins bons que ceux de BalancedBagging ou de MarginBoost car ils essaient d’obtenir le meilleur taux de classification moyen sur toute la base. Les heuristiques qu’ils engendrent sont donc les meilleurs compromis possibles afin d’obtenir ce plus haut taux. Mais ClusteredSampling a été créé dans une autre optique : engendrer des règles précises pour quelques groupes d’instances seulement. Pertinent pour une minorité de cas, son taux de classification reste moins bon pour la totalité des instances. Il est donc impératif pour cet algorithme de connaître les limites de validités de sa réponse (voir Assemblée de classifieurs).

L’algorithme est sensible au nombre de groupes d’instances. Plus il y a de groupes, plus les règles apprises sont fines mais plus valables que pour certaines instances. L’algorithme en est d’autant plus instable.

De plus le rééquilibrage des instances de chaque groupe se fait automatiquement ce qui avantage les instances de la classe majoritaire du fait de la redondance des instances (même problème survenu pour les autres classifieurs). Ceci montre que le rééquilibrage n’est pas pertinent est qu’une amélioration est à apporter à cet algorithme.

4) Assemblée de classifieurs.

L’alliance des classifieurs n’améliore que faiblement les performances individuelles contrairement à ce qui était attendu (cf. tableau 11). Le routeur a les mêmes problèmes que les classifieurs en apprentissage : le bruit de la base les entraîne à faire des compromis en généralisation pour avoir un fort taux de classification. Aussi, le réglage correct de chacun d’eux pour améliorer les performances reste difficile du fait du nombre important de paramètres du système.

L’apprentissage du routeur est fortement lié au nombre de bases d’apprentissage en validations croisées. Plus le nombre de bases est grand, plus les bases d’apprentissage sont importantes et plus le routeur aura tendance à faire confiance aux classifieurs qui auront appris par cœur ces données. A contrario, moins il y aura de bases, plus elles seront petites et plus le routeur prendra de distance sur les décisions des classifieurs qui auront moins bien appris. Un juste compromis est nécessaire. Ici un optimum est trouvé pour 7 bases et le résultat est meilleur que ceux de chaque classifieurs pris séparément.

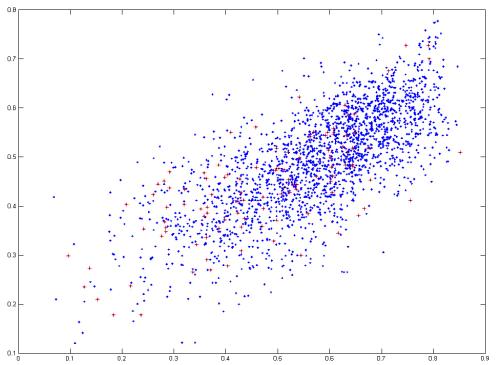
La comparaison entre la prédiction des classifieurs et celle du routeur montre la façon dont celui-ci accorde un degré de confiance à chacun. Dans cet exemple, ses prédictions restent corrélées à celles de l’algorithme BalancedBagging (cf. figure 3). L’information que lui apporte les deux autres classifieurs (cf. figures 4, 5) semble lui être moins utile. Ici MarginBoost a été mal paramétré : il classifie toutes les instances comme appartenant à la classe minoritaire. Le routeur corrige ses prédictions en les surestimant.

3 Etude des erreurs de classification.

Un fait intéressant surgit lorsque l’on observe les erreurs faites par les deux classifieurs. BalancedBagging et MarginBoost se trompent quasiment toujours sur les mêmes instances indépendamment de leurs paramètres d’initialisation, c'est-à-dire 400 instances de la classe négative et 25 de la classe positive. Nous avons voulu essayer de comprendre pourquoi ces instances posaient problème en dégageant leurs attributs les plus caractéristiques en les regroupant par quantification vectorielle (cf. annexe, étude des erreurs de classifications) : 6 groupes distincts de la classe EVENT ne sont jamais appris par les classifieurs.

L’étude de ces groupes par les médecins associés au projet a montré que ces instances de la classe EVENT possédaient « une caractéristique commune rare mais à forte valeur prédictive » (en l’occurrence l’attribut booléen des antécédents d'infarctus myocardique). Sur l’ensemble de la base, 4% des patients ont eu un infarctus et se répartissent ainsi : 3.5% pour la classe majoritaire et 0.5% pour la classe minoritaire.

Ce constat dévoile une chose qui n’avait pas été comprise jusqu’alors: la distribution de la base INDANA est caractérisée par un déséquilibre interclasse mais aussi par des déséquilibres intraclasses. Certaines instances ultra-minoritaires dans leur propre classe ne sont jamais apprises. Il est donc maintenant compréhensible pourquoi les classifieurs se trompent toujours sur ces instances. Ils n’ont pas été étudiés pour résoudre le déséquilibre intraclasse.

Le rajout dans la base des barycentres des groupes de ces instances améliore les performances prédictives des classifieurs (cf. techniques de rééquilibrage de données). Ceci prouve bien l’existence du déséquilibre intraclasse.

Cette étude a permis en outre l’élaboration de l’algorithme ClusteredSampling et le choix d’employer les arbres de classifieurs.

VI Conclusion et perspectives.

Nous avons proposé plusieurs extensions d’algorithmes de combinaison de classifieurs pour le problème de déséquilibre entre les distributions : BalancedBagging, un algorithme de Bagging « rééquilibré », « Cost-Sensitive MarginBoost », un algorithme de Boosting sensible aux coûts et «ClusteredSampling » un algorithme de classification par segmentation. Nous avons évalué leurs performances sur la base INDANA et montré leur efficacité en les comparant à d’autres algorithmes existants. Nous avons ensuite appliqué un méta-classifieur sur les algorithmes et montré qu’un gain est possible. Cette étude empirique doit maintenant être poursuivie par une étude théorique de leurs propriétés respectives.

L’analyse, par les médecins associés au projet, des données mal classées a permis de mettre en évidence le fort déséquilibre intraclasse de la base et aussi la difficulté qu’ont les algorithmes proposés à s’en défaire. Si ClusteredSampling n’a apporté aucun gain de performance par rapport aux deux autres méthodes, il serait intéressant de continuer les recherches sur celui-ci car des améliorations restent à faire comme un rééquilibrage pertinent des groupes d’instances. La méthode de réétiquetage d’instances garantissant un biais minimal utilisé par Elkan pour son algorithme Cost-Sensitive Decision Making [9] peut être une réponse à ce problème.

D’autres voies sont à explorer comme étendre l’application de ces algorithmes à l’apprentissage semi-supervisé : garder les étiquettes des instances les plus caractéristiques de leur classes et retirer celles à la frontière de décision. Du fait du bruit important dans les données, ceci peut améliorer leurs performances, de même que leur utilisation pour le problème de la régression.

L’arbre de classifieur améliore légèrement la performance globale sur cette base-ci. Il renseigne de plus sur la pertinence des modèles et modifie leurs prédictions. Il faut poursuivre les études sur ces algorithmes pour le problème du déséquilibre entre les distributions des classes.

Chacun des algorithmes présentés pondèrent par un coût fixe les erreurs de classification. Un développement futur pourrait être la généralisation de ces algorithmes à un coût d’erreur variable. Une piste qui a été étudiée par Elkan [9]…

VII Bibliographie.

[1] Bishop 1995 Neural Networks in Pattern Recognition.

[2] Breiman 1994 Bagging Predictors. TechnicalReportNo.421.

[3] Chan & Stolfo 1999 AdaCost: Misclassication Cost-sensitive Boosting Proc. 16th InternationalConf. On Machine Learning

[4] Catlett, 1991 MegaInduction: Machine learning on very large databases. PhD. Thesis, School of computer Science, University of Technology, Sydney, Australia.

[5] Chawla, Moore, Hall, Springer, KegelMeyer 2001 Bagging-like effects for Decision trees and Neural Nets in Protein Secondary Structure Prediction. BIOKDD2001: Workshop on Data Mining in Bioinformaitics (SIGKDD01 Conference).

[6] D’Alché-Buc, Grandvalet & Ambroise 2001 Semi-Supervised MarginBoost, PrePrint NIPS’01.

[7] Domingos 2001 MetaCost: A General Method To Make Classifiers Cost-Sensitive, Knowledge Discovery and Data Mining, p155-164.

[8] Elkan 2001 The Foundations of Cost-Sensitive Learning, IJCAI, 973-978.

[9] Elkan & Zadrozny 2001 Learning and Making Decisions When Costs and Probabilities are Both Unknown, Knowledge Discovery and Data Mining, 204-213.

[10] Ezawa 1996 Learning goal oriented bayesian networks for telecom risk management. Proceedings of IMCL-96, 139-147. San Francisco, CA: Morgan Kaufmann.

[11] Freund, Boosting a weak learning algorithm by majority, Information and Computation, 121(2):256{285, 1995.

[12] Friedman 1999 Stochastic Gradient Boosting.

[13] Haykin 1998 Neural Networks.

[14] Heckman 1979 Sample selection Bias as a specification error, Econometrica, 47:153-161.

[15] Japkowicz 2000 The class imbalance problem: Significance and strategies, In Papers from the AAAI Workshop on Learning from Imbalanced Data Sets. Tech. rep. WS-00-05, Menlo Park, CA: AAAI Press

[16] Kubat & Matwin 1997 Addressing The Curse Of Imbalanced Training Set: One-Sided Selection, Proc. 14th International Conference on Machine Learning, p179-186

[17] A. Iwata, S. Kuroyanagi, S. Nugroho 2002 A Solution For Imbalanced Training Sets Problem by CombNET II and its Application on Fog ForeCasting. IEICE, Transf. Inf. & Syst. Vol. E-85D, No. 7 july 2002

[18] Mason, Baxter, Barlett & Frean 1999 Boosting Algorithms as Gradient Descent in Function Space, Technical report, RSISE, Australian

[19] Lewis & Catlett 1994. Heterogenous uncertainty sampling for supervised learning. Proceedings of 11^th ICML, 148-156. San Francisco, CA: Morgan Kaufmann.

[20] Pazzani et al. 1994 Reducing Misclassification Costs. Proceedings of the 11^th International Conference on Machine Learning, (ICML 94, p217-225).

[21] Provost 2000 Machine Learning from Imbalanced Data Sets 101

[22] Ridgeway 1999 The State of Boosting

[23] Schapire & Freund 1996 Experiments With a New Boosting Algorithm, International Conference on Machine Learning, p148-156

[24] Sung & Poggio 1998 Example-based learning for view-based face detection, IEEE Trans., PAMI 20, 39-51.

[25] Ting An Empirical Study of MetaCost using Boosting, Proceedings ECML 2000, 11th European Conference on Machine Learning, p413-425.

[26] Turney 1997 Types of Cost in Inductive Concept Learning, Workshop on Cost-Sensitive Learning at ICML2000, Stanford University, California, 15-21.

[27] Vucetic & Obradovic 2000 Performance Controlled Data Reduction for Knowledge Discovery in Distributed Databases, Pacific-Asia Conference on Knowledge Discovery and Data Mining, p29-39.

[28] Weiss & Provost 2001 The Effect of Class Distribution on Classifier Learning: An Empirical Study, Technical Report ML-TR 43, Department of Computer Science, Rutgers University

VIII Annexe.

1 Présentation des attributs et de la base de données.

La base de données INDANA comporte 2229 instances de 18 attributs sans valeur manquante. Les instances sont classées binairement « événement réalisé » (classe EVENT) et « événement non réalisé » (classe NO_EVENT) distribuées ainsi :

2122 instances de la classe NO_EVENT (95.20% de la base)

107 instances de la classe EVENT (4.80% de la base)

Les 18 attributs correspondent à des caractéristiques et à des mesures prises chez chaque patient :

Paramètre Unité de mesure Commentaires

Le sexe booléen valeur binaire, non ordonné

L’âge année valeur continue, entier

La taille en début d’étude centimètre valeur continue, entier

Le poids en début d'étude kg valeur continue, entier

Les antécédents de diabète booléen valeur binaire, ordonné

La fréquence cardiaque en début d'étude battement/min valeur continue, entier

La pression artérielle systolique en début d'étude mmHg valeur continue, entier

La pression artérielle diastolique en début d'étude mmHg valeur continue, entier

Le code Minnesota ECG en début d'étude catégorie valeur non ordonné

Le code Minnesota ECG en début d'étude catégorie valeur non ordonné

Le code Minnesota ECG en début d'étude catégorie valeur non ordonné

Le cholestérol total en début d'étude mmol/l valeur continue, réel

Les antécédents d'infarctus myocardique booléen catégorie binaire, ordonné

Les antécédents d'AVC booléen catégorie binaire, ordonné

Le tabagisme (statut actuel) en début d'étude booléen catégorie binaire, ordonné

Le délai jusqu'au décès années valeur continue, réel

Le décès cardio-vasculaire booléen catégorie binaire, ordonné

L’index pondéral en début d'étude kg/m² valeur continue, réel

Indicateur de valeur manquante booléen catégorie binaire, ordonné

Le paramètre du délai jusqu’au décès qui n’est connu qu’à la fin de l’étude n’est pas pris en compte dans les expérimentations faites.

Le décès cardio-vasculaire représente la catégorie d’appartenance du patient. Ce paramètre sera pour nous la classe de l’instance que l’on aura à prédire en apprentissage supervisé. C’est un attribut booléen qui indique la réalisation ou non de l’événement «décès cardio-vasculaire ». Les autres attributs seront nos paramètres d’entrée.

2 Algorithmes existants.

1) MetaCost.

Tableau 1 Influence du coût d’erreur sur la classe minoritaire sur l’apprentissage avec 30 arbres de décision.

Coût d’erreur associé à la Classe 1	10	20	30	35	36	36.3	37	40
Rappel 0	0.959	0.836	0.779	0.615	0.539	0.521	0.467	0.168
Rappel 1	0.15	0.308	0.327	0.551	0.598	0.617	0.645	0.82
Précision 0	0.957	0.836	0.958	0.964	0.964	0.964	0.963	0.955
Précision 1	0.157	0.308	0.069	0.067	0.061	0.061	0.058	0.049
Fmesure 0	0.958	0.894	0.859	0.751	0.691	0.676	0.629	0.302
Fmesure 1	0.153	0.135	0.114	0.12	0.111	0.111	0.106	0.092

2) AdaCost.

Tableau 2 Influence du coût d’erreur sur la classe minoritaire sur l’apprentissage avec l’algorithme 30 classifieurs SMO.

Coût d’erreur associé à la Classe 1	25	26	27	28	30
Rappel 0	0.672	0.646	0.602	0.598	0.583
Rappel 1	0.617	0.617	0.645	0.701	0.654
Précision 0	0.972	0.971	0.972	0.975	0.971
Précision 1	0.087	0.081	0.079	0.081	0.073
Fmesure 0	0.795	0.776	0.758	0.741	0.729
Fmesure 1	0.795	0.145	0.141	0.145	0.132

3) CSB.

Tableau 3 Influence du coût d’erreur sur la classe minoritaire sur l’apprentissage avec 30 classifieurs SMO.

Coût d’erreur associé à la Classe 1	10	15	17	19.7	20	22	30
Rappel 0	0.99	0.989	0.99	0.792	0.293	0.101	0.004
Rappel 1	0	0.011	0.009	0.206	0.71	0.897	1
Précision 0	0.952	0.952	0.952	0.952	0.953	0.951	1
Précision 1	0	0.08	0.045	0.047	0.048	0.048	0.048
Fmesure 0	0.97	0.97	0.971	0.864	0.448	0.182	0.008
Fmesure 1	0	0.03	0.016	0.077	0.09	0.091	0.092

3 Nouveaux algorithmes.

1) BalancedBagging.

Tableau 4 Influence de la proportion de la classe majoritaire sur l’apprentissage avec 10/20/30 classifieurs J48 (arbres de décision).

Rapport Classe 0 / Classe 1	(95%) 19.83 Bagging	(4%) 0.8	(3.8%) 0.775	(3.75%) 0.75	(3.5%) 0.7
Rappel 0	0.999/1/1	0.599/0.609/0.623	0.599/0.631/0.641	0.591/0.599/0.607	0.577/0.58/0.573
Rappel 1	0.009/0/0	0.57/0.654/0.636	0.654/0.654/0.645	0.682/0.645/0.729	0.645/0.626/0.673
Précision 0	0.952/0.952/0.952	0.965/0.972/0.971	0.972/0.973/0.973	0.974/0.971/0.978	0.97/0.969/0.972
Précision 1	0.25/0/0	0.067/0.078/0.078	0.076/0.082/0.083	0.078/0.075/0.086	0.071/0.07/0.074
Fmesure 0	0.975/0.975/0.975	0.74/0.749/0.759	0.741/0.766/0.773	0.735/0.741/0.749	0.723/0.726/0.721
Fmesure 1	0.018/0/0	0.12/0.139/0.14	0.136/0.146/0.147	0.139/0.135/0.153	0.128/0.126/0.133

Tableau 5 Influence de la proportion de la classe majoritaire sur l’apprentissage avec 10/20/30 classifieurs SMO (Machines à vecteurs de support).

Rapport Classe0 / Classe1	(5%) 1	(4.5%) 0.9	(4.25%) 0.85	(4%) 0.8	(3.8%) 0.775
Rappel 0	0.701/0.736/0.735	0.642/0.658/0.658	0.639/0.651/0.661	0.556/0.584/0.597	0.535/0.532/0.554
Rappel 1	0.579/0.551/0.542	0.636/0.626/0.645	0.645/0.654/0.626	0.701/0.673/0.654	0.738/0.701/0.701
Précision 0	0.971/0.449/0.97	0.972/0.972/0.974	0.973/0.974/0.972	0.974/0.973/0.972	0.976/0.972/0.973
Précision 1	0.089/0.264/0.094	0.082/0.085/0.087	0.083/0.086/0.085	0.074/0.075/0.076	0.074/0.07/0.073
Fmesure 0	0.814/0.837/0.836	0.774/0.785/0.785	0.772/0.78/0.787	0.708/0.73/0.739	0.691/0.688/0.706
Fmesure 1	0.154/0.162/0.16	0.146/0.149/0.153	0.147/0.153/0.15	0.133/0.136/0.136	0.135/0.128/0.133

Tableau 6 Etude des marges d’erreurs faites par BalancedBagging

565 instances mal classées

537 de la classe NO_EVENT

28 de la classe EVENT

Taux de prédiction du classifieur	Instances mal classées Classe 0	Instances mal classées Classe 1
> 99%	14	1
> 90%	24	0
> 80%	58	3
> 70%	89	8
> 60%	150	7
> 50%	202	9

2) Cost-Sensitive MarginBoost.

Tableau 7 Influence de la proportion de la classe majoritaire sur l’apprentissage avec le classifieur J48 (arbres de décision).

Coût d’erreur sur la classe 1	1	150	200	250	300
Rappel 0	1	0.687	0.618	0.525	0.519
Rappel 1	0	0.458	0.533	0.636	0.664
Précision 0	0.952	0.962	0.963	0.966	0.968
Précision 1	0	0.069	0.066	0.063	0.065
Fmesure 0	0.975	0.802	0.753	0.68	0.676
Fmesure 1	0	0.12	0.117	0.115	0.119

Tableau 8 Influence de la proportion de la classe majoritaire sur l’apprentissage avec le classifieur SMO (Machines à vecteurs de support).

Coût d’erreur sur la classe 1	22	23	24	26	30
Rappel 0	0.672	0.631	0.607	0.557	0.463
Rappel 1	0.542	0.617	0.626	0.701	0.757
Précision 0	0.967	0.97	0.97	0.974	0.974
Précision 1	0.542	0.078	0.074	0.074	0.066
Fmesure 0	0.793	0.765	0.746	0.709	0.627
Fmesure 1	0.135	0.138	0.133	0.134	0.122

Tableau 9 Etude des marges d’erreurs faites par Cost-Sensitive MarginBoost

570 instances mal classées

546 la classe NO_EVENT

24 la classe EVENT

Taux de prédiction du classifieur	Instances mal classées Classe 0	Instances mal classées Classe 1
> 99%	419	23
> 80%	65	0
> 70%	27	0
> 60%	19	0
> 50%	16	1

3) ClusteredSampling.

Tableau 10 Influence du nombre de clusters sur l’apprentissage de L’algorithme BalancedBagging avec 30 classifieurs SMO (Machines à vecteurs de support).

Nombre de Clusters	2	3	4	7	10
Rappel 0	0.68	0.738	0.775	0.68	0.712
Rappel 1	0.589	0.551	0.439	0.421	0.402
Précision 0	0.97	0.97	0.965	0.959	0.959
Précision 1	0.085	0.096	0.09	0.062	0.066
Fmesure 0	0.8	0.838	0.86	0.796	0.818
Fmesure 1	0.148	0.163	0.149	0.108	0.113

4) Assemblée de classifieurs.

Tableau 11 Influence du nombre de bases en validation croisée

Algorithme BalancedBagging de 30 classifieurs J48 avec un rééquilibrage de 1.

Algorithme ClusteredSampling de 4 clusters.

Algorithme MarginBoost de 30 classifieurs SMO avec un coût d’erreur de 23.

Routeur :

Algorithme BalancedBagging de 30 classifieurs J48 avec un rééquilibrage de 0.775.

Nombre de bases pour la validation croisée	3	5	7	8	10
Rappel 0	61.6	0.634	0.637	0.623	0.631
Rappel 1	0.598	0.598	0.692	0.664	0.579
Précision 0	0.968	0.969	0.976	0.974	0.968
Précision 1	0.073	0.076	0.088	0.082	0.073
Fmesure 0	0.753	0.766	0.771	0.76	0.764
Fmesure 1	0.13	0.135	0.156	0.145	0.13

4 Etude des erreurs de classification des classifieurs BalancedBagging et Cost-Sensitive MarginBoost.

1) Caractéristiques des instances mal apprises.

6 groupes caractéristiques composent les 32 instances la classe EVENT sur lesquels les classifieurs se trompent toujours.

Groupe 1 4 patients (13% des 32 patients) homme type 1

Male 77.75 170.25 76.75 NO 72.0 163.5 69.25 0.0 0.25 1.0 5.1925 YES NO NOT_SMOKER 3.655 EVENT SHEP 27.0 0.0

Groupe 2 6 patientes (19% des 32 patients) femme type 1

Female 75.0 158.5 68.83 NO 72.33 168.66 75.0 0.33 0.0 2.0 6.34 YES NO NOT_SMOKER 4.54 EVENT SHEP 27.16 0.0

Groupe 3 5 patientes (16% des 32 patients) femme type 2 (fumeuse)

Female 77.2 154.2 58.8 YES 68.4 169.2 73.6 0.0 0.0 0.0 6.66 YES NO NOT_SMOKER 4.042 EVENT SHEP 24.4 0.0

Groupe 4 5 patientes (16% des 32 patients) femme type 3

Female 73.4 158.0 59.0 NO 71.6 172.8 78.8 0.0 0.0 0.8 6.056 YES NO CURRENT_SMOKER 4.386 EVENT SHEP 23.8 0.0

Groupe 5 10 patients (31% des 32 patients) homme type 2

Male 74.4 172.0 85.0 NO 72.8 173.6 79.8 0.1 0.0 0.0 6.071 YES NO NOT_SMOKER 4.18 EVENT SHEP 28.6 0.0

Groupe 6 2 patients (6% des 32 patients) homme type 3

Male 63.0 156.0 58.0 NO 86.0 166.5 63.0 0.5 1.0 2.0 6.055 YES NO NOT_SMOKER 4.855 EVENT SHEP 24.0 0.0

2) Analyse des prédictions des classifieurs.

1) Algorithmes seuls.

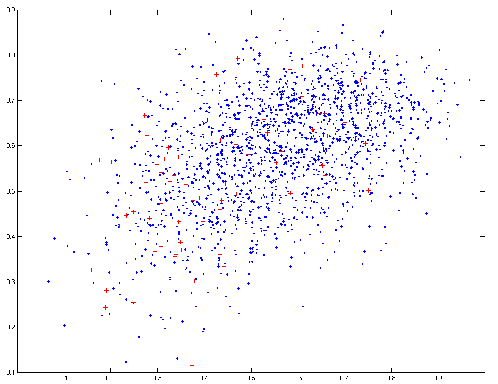
Figure 1 Prédiction de BalancedBagging en abscisse et de Marginboost en ordonnée en la classe NO_EVENT pour chaque instance (Bleu : NO_EVENT ; Rouge : EVENT).

Figure 2 Prédiction de BalancedBagging en abscisse et de ClusteredSampling en ordonnée en la classe NO_EVENT pour chaque instance (Bleu : NO_EVENT ; Rouge : EVENT).

2) Combinaison d’algorithmes.

Arbre de 3 classifieurs ClusteredSampling, BalancedBagging et MarginBoost. Le routeur est un classifieur BalancedBagging.

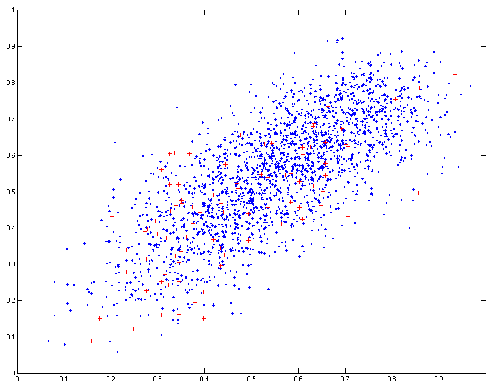
Figure 3 Prédiction de BalancedBagging en abscisse et du routeur en ordonnée en la classe NO_EVENT pour chaque instance (Bleu : NO_EVENT ; Rouge : EVENT).

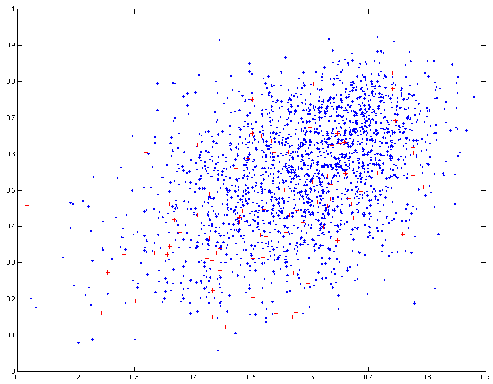
Figure 4 Prédiction de ClusteredSampling en abscisse et du routeur en ordonnée en la classe NO_EVENT pour chaque instance (Bleu : NO_EVENT ; Rouge : EVENT).

Figure 5 Prédiction de MarginBoost en abscisse et du routeur en ordonnée en la classe NO_EVENT pour chaque instance (Bleu : NO_EVENT ; Rouge : EVENT).

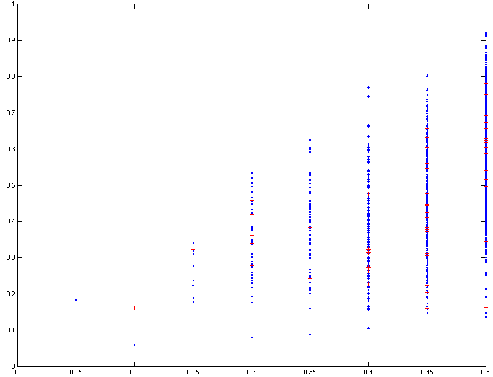
Figure 6 Prédiction de deux classifieurs en la classe NO_EVENT pour chaque instance

(Bleu : NO_EVENT ; Rouge : EVENT)