Base 10 et numérotation de position
Dans le système décimal, nous utilisons 10 symboles : 0,1,2,3,4,5,6,7,8,9 et la position d'un symbole correspond au chiffre des unités, des dizaines, des centaines, etc.
Codage binaire
En informatique, la base la plus utilisée est la base 2 avec donc deux symboles, 0 et 1.
Le principe général de codage est alors le suivant : si (an-1,an-2,...,a0)2 dénote un nombre en base 2, sa valeur décimale est :
Comme nous l'avons vu avec les tables de vérité, un alphabet de deux lettres permet d'écrire 2n mots différents de taille n.
Avec le codage précédent, ces valeurs correspondent aux entiers de 0 à 2n-1.
Remarque : le bit à la position 0, dit bit de poids faible, détermine à lui seul la parité de l'entier à représenté : s'il vaut 0, le nombre est pair, s'il vaut 1, le nombre est impair.
Conversion par divisions successives
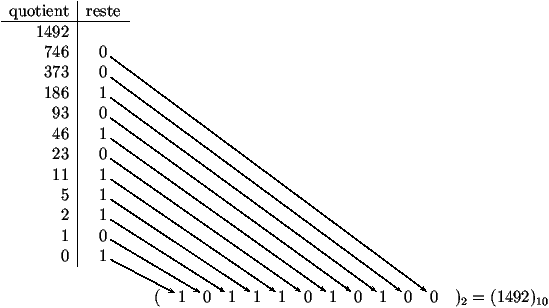
La figure 2.1 montre le principe de conversion (par divisions successives) de la base 10 vers la base 2. Pour passer d'un nombre décimal à un nombre octal ou hexadécimal, le même principe peut être appliqué.
Opérations arithmétiques en binaire
L'addition en base 2
À nouveau, nous pouvons définir les opérations élémentaires par analogie avec le système décimal. L'addition en binaire de deux nombres consiste à effectuer l'addition binaire sur les bits de même poids de chaque nombre reportant de droite à gauche les retenues successives.
Un exemple d'addition simple (car elle n'implique pas de retenue) est :
| 1 | 0 | 1 | 1 | |
| + | 0 | 1 | 0 | 0 |
|
| ||||
| 1 | 1 | 1 | 1 | |
Un peu plus compliqué :
| 1 | 1 | |||
| 0 | 0 | 1 | 0 | |
| + | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | |
Et enfin :
| 1 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | |
| + | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | |
On peut résumer ces opérations à l'aide d'une table de vérité comme vu dans le cours de logique :
| a | b | résultat de (a+b) | retenue de (a+b) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Si l'on convient que 1 correspond à vrai et 0 à faux, il apparaît que l'addition correspond à l'opérateur booléen XOR (OU-exclusif) et que la retenue peut elle être calculée à l'aide de l'opérateur ET.
Multiplication et division
Notons simplement qu'il est facile de multiplier et diviser par la base utilisée : en base 10, multiplier par 10 revient à ajouter un zéro à la droite du nombre (décalage à gauche), tandis que diviser revient à supprimer un chiffre à droite (décalage à droite).
Cela est encore vrai en base 2. Par exemple, on pourra vérifier aisément que 1011 multiplié par 2 vaut 10110 et que le même nombre divisé par 2 donne 101.
Autres bases
Dans un système à base k, il faut k symboles. En informatique, la base la plus utilisée est la base 2 avec deux symboles, 0 et 1, mais on utilise également la base 8 (système octal) et la base 16 (système hexadecimal).
| nom du codage | base | symboles |
|---|---|---|
| binaire | 2 | 0,1 |
| octal | 8 | 0,1,2,3,4,5,6,7 |
| hexadécimal | 16 | 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F |
Le principe général de codage est le suivant : si (an-1,an-2,...,a0)b dénote un nombre en base b, sa valeur décimale est
Le principe des divisions successives est toujours valable, quelle que soit la base utilisée. Cependant, il existe une méthode dite par regroupements qui est valide pour les bases qui sont des puissances de 2. C'est le cas de la base 8 (8 = 23) et de la base 16 (16 = 24).
Cette méthode nous permet de passer de la base 2 à une autre base, puissance de 2. Dans le cas d'un passage à la base 8, les bits sont regroupés par 3 et décodés. Au besoin, nous pouvons rajouter des 0 à gauche. Voyons cela pour le changement de base du nombre binaire (10111010100)2 :
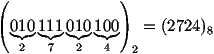
Pour passer à la base 16, nous appliquons le même procédé en regroupant cette fois les bits 4 par 4 :
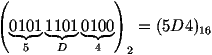
Dispositifs physiques pour coder deux valeurs
Représentation des entiers relatifs
Première tentative de codage
Nous avons vu dans les sections précédentes un codage simple qui, en utilisant n bits permet de représenter les entiers naturels compris entre 0 et 2n-1.
Il s'agit maintenant de trouver un codage (et le décodage correspondant) qui permette en plus de représenter des entiers négatifs.
La première idée consiste à utiliser le bit de poids fort pour coder le signe de l'entier tandis que les autres bits codent la valeur absolue de l'entier en utilisant le codage binaire vu précédemment.
Par exemple, en codage binaire habituel, le mot 011 code la valeur 3 ; avec notre proposition de codage des entiers relatifs, nous aurions, sur 4 bits, 0011 qui code toujours la valeur 3 et 1011 qui représenterait la valeur -3.
Ce codage présente au moins deux inconvénients sérieux :
- le zéro possède deux représentations ; ainsi, sur 4 bits, on a 0000 et 1000 ;
- l'addition telle que nous l'avons définie n'est plus valide pour ce codage ; par exemple, sur 4 bits, 0010 + 1001 (c'est-à-dire 2-1) donne 1011 (autrement dit, le résultat de 2-1 vaut -3).
C'est pourquoi un autre codage a été présenté : le codage en complément à 2.
Codage en complément à 2
La formule proposée pour décoder un mot binaire en valeur décimale est la suivante :
La différence avec le codage binaire habituel se fait sur le bit de poids fort qui code une valeur négative d'une puissance de 2. Si ce bit de poids fort vaut 0, il s'agit donc nécessairement d'un entier positif ; en revanche, un bit de poids fort à 1 désigne un entier négatif.
La formule montre que les autres bits codent une valeur avec la convention habituelle du codage binaire mais, contrairement à la première idée exposée ci-dessus, ces bits ne codent pas la valeur absolue de l'entier mais son complément par rapport à la puissance de 2 du bit de poids fort.
Codons par exemple la valeur -3, toujours sur 4 bits :
- le bit de poids fort vaut 1 car -3 est négatif ;
- les autres bits nous permettent de coder, non pas, la valeur 3 mais la valeur de 23-3, soit 5. Ce codage peut être trouvé par la méthode des divisions successives.
Le codage de -3 en complément à 2 est donc 1101.
Reprenons notre exemple d'addition : 0010 + 1001 = 1011. Le premier nombre binaire dénote toujours la valeur décimale 2, le deuxième représente maintenant -7 et la dernière -5 : 2 - 7 = -5, notre addition est de nouveau valide !
Une méthode générale pour coder un entier en complément à 2 est donnée par l'algorithme suivant :
- convertir a en binaire en utilisant n-1 bits (par exemple, par la méthode des divisions successives) ;
- ajouter un 0 à gauche ;
- remplacer les 0 par des 1 et les 1 par des 0 ;
- ajouter 1.
Reprenons comme exemple le codage de -3 en complément à 2 sur 4 bits :
- en binaire, la valeur 3 est représentée sur 3 bits par le mot 011 ;
- l'ajout d'un 0 à gauche nous donne le mot 0011 ;
- l'inversion des bits nous fournit le mot 1100 ;
- enfin l'ajout de 1 à ce nombre nous donne, comme attendu, 1101.
Cette fois, les entiers représentables avec des mots de n bits sont ceux compris entre -2n-1 et 2n-1-1. À noter que le nombre de valeurs différentes représentables avec n bits reste naturellement de 2n.
Codages des caractères
Principes de quelques codages
La première étape consiste définir le jeu de caractères : il s'agit simplement de lister les caractères que nous voulons pouvoir représenter et à les numéroter.
Ensuite, vient l'étape du codage : décider comment les numéros associés aux caractères vont être représentés par des bits. Quelle que soit la langue visée, une réflexion rapide amène à un jeu d'une centaine de caractères. On peut donc légitimement proposer un codage binaire classique sur 7 bits puisque celui-ci autorise 128 valeurs distinctes.
Dans les années 60, ce type de réflexion a conduit à la définition du codage ASCII (pour American Standard for Communication and International Interchange). L'association entre les lettres et leurs numéros n'est cependant pas arbitraire :
A 65 100 0001
. .. ... ....
. .. ... ....
. .. ... ....
. .. ... ....
Z 90 101 1010
. .. ... ....
. .. ... ....
a 97 110 0001
b 98 110 0010
. .. ... ....
. .. ... ....
. .. ... ....
. .. ... ....
z 122 111 1010
On note qu'une lettre majuscule se trouve à 32 de sa version minuscule. Autrement dit, il suffit de changer le bit de position 5 pour passer de l'une à l'autre.
Ces 128 caractères proposés par l'ASCII sont finalement loin d'être suffisants. Les caractères ASCII sont codés sur 7 bits mais utilisaient un 8ème bit de contrôle. Les codes ASCII étendus utilisent ce bit supplémentaire pour doubler le nombre de caractères représentables (au nombre de 256 donc). Les 128 premiers caractères restent ceux disponibles en ASCII ce qui permet une compatibilité dans les deux sens.
Parmi eux, on trouve le ISO-8859-1 ou ISO-Latin-1 dédié aux langues de l'Europe de l'Ouest. Une variation sur cette norme est l'ISO-8859-15 qui intègre le symbole euro et le e dans l'o. D'autres codes ASCII étendus :
- windows-1252 : une variation windowzienne sur le ISO-Latin-1... à éviter ;
- ISO-8859-2 : langues de l'Europe Centrale et de l'Est ;
- ISO-8859-3 : esperanto, maltais et turc ;
- ISO-8859-4 : langues baltes ;
- ISO-8859-5 : alphabet cyrillique ;
- ISO-8859-6 : arabe ;
- ISO-8859-7 : grec moderne ;
- ISO-8859-8 : hébreu et yiddish ;
- etc.
Vient ensuite la difficulté de mélanger toutes ces langues, pour des documents incluant des traductions par exemple. Le jeu de caractères UNICODE a été conçu dans cet esprit. On y trouve plus de 95 000 caractères représentant quasiment toutes les langues vivantes ou mortes. Par exemple, le caractère numéro 12354 correspond au A dans l'alphabet japonais Hiragana (あ).
Il y a plusieurs moyens de coder ce jeu de caractères :
- l'UTF-16 : codage des caractères de UNICODE sur 16 bits ; on perd la compatibilité avec ASCII et un fichier peut occuper le double de sa place idéale si le texte est monolingue ;
- l'UTF-8 répond à ces deux difficultés en utilisant un nombre variable de bits selon le numéro
du caractère à coder :
- de 0 à 127 (caractères ASCII) : un octet de la forme 0xxx xxxx;
- de 128 à 2047 : deux octets de la forme 110x xxxx 10xx xxxx;
- de 2048 à 65 535 : trois octets de la forme 1110 xxxx 10xx xxxx 10xx xxxx;
- de 65 536 à 1 114 111 : quatre octets de la forme 1111 0xxx 10xx xxxx 10xx xxxx 10xx xxxx.
À noter que l'UTF-8 est le codage privilégié des langages XML.
Codage des caractères : un exemple
On considère la chaîne de caractères « hé ! », soient 4 caractères dont les numéros en UNICODE et ISO-LATIN1 sont : 104, 233, 32 et 33. Une fois ces entiers codés en binaire sur 8 bits, nous obtenons :
- 104 : 0110 1000
- 233 : 1110 1001
- 32 : 0010 0000
- 33 : 0010 0001
Codages en iso-latin1 et utf-8
En iso-latin-1, on met bout à bout et l'on obtient :
En Utf-8, tous les caractères sauf é vont être codés par un octet et restés semblables au codage latin1.
En revanche, le code du é, 233, est compris entre 128 et 2047, il nécessite donc deux octets avec le motif suivant : 110x xxxx - 10xx xxxx. La méthode consiste à reprendre 233 codé en binaire (1110 1001), à l'étendre sur 11 bits (000 1110 1001) et à distribuer ces bits dans les emplacements libres du motif. Ce qui donne au final :
Décodages possibles de ces chaînes binaires
On regarde le processus inverse : obtenir des caractères à partir du binaire.
Tout d'abord, latin1 interprété en latin1 :
interprété en iso-8859-15, on décode octet par octet et cela donne la suite d'entiers 104 - 233 - 32 - 33, qui représente bien le texte attendu « hé ! ».
Ensuite, regardons de l'utf8 interprété en utf8 :
Les deuxième et troisième octets ne commencent pas par 0, il faut par conséquent prendre en compte l'enveloppe UTF-8 :
Elle nous indique que le caractère utilise 2 octets (110xxxxx) ; les données restantes sont donc :
soit l'entier 233, correspond au é, on retrouve à nouveau les entiers 104 - 233 - 32 - 33 et le texte « hé ! ».
On regarde maintenant le cas où le codage latin1 est interprété en utf8 :
interprété en utf8, 1110 1001 annonce l'arrivée de deux octets commençant par 10, or les deux suivants commencent par 00 : une incohérence est détectée, il n'y aura pas de décodage possible.
Problème inverse, on essaye d'interpréter de l'utf8 en latin1 :
interprété en iso-8859-15, on décode octet par octet, on trouve les entiers 104 - 195 - 169 - 32 - 33, soit le texte « hé ! ».
Terminons par du latin1 interprété en utf16 :
interprété en utf16, les octets sont lus deux par deux et le décodage fournit donc deux entiers :
- 0110 1000 - 1110 1001 : 26 857
- 0010 0000 - 0010 0001 : 8 225
c'est-à-dire le texte « 棩‡ ».
Codages des couleurs en RGB
Une couleur codée en RGB (Red Green Blue) se présente comme un nombre hexadécimal à six chiffres : FF06C3 par exemple. Chaque paire de chiffres est dédiée à une couleur primaire. Sur le même exemple, cela donne :
- FF pour le rouge ;
- 06 pour le vert ;
- C3 pour le bleu ;
soit les valeurs décimales 255, 6 et 211. Chacune de ces valeurs indique l'intensité avec laquelle la lampe correspondant va être allumée. Puisque FF soit 255 est le maximum représentable sur deux chiffres en hexadécimal, on déduit :
- 100 % pour la lampe rouge ;
- 2,35 % pour la lampe verte ;
- 82,75 % pour la lampe bleue.
Toutes les lampes au maximum de leur intensité (FFFFFF) fournissent du blanc, alors que toutes les lampes éteintes (000000) font naturellement du noir.
