Préliminaires

L'application aux jeux a toujours été un domaine actif de l'Intelligence Artificielle. On s'intéresse ici aux jeux asynchrones opposant deux joueurs (chacun joue à son tour), à information complète (chacun sait tout de la situation de jeu, à chaque instant).

Dans la suite, on note J₁ et J₂ les deux joueurs et l'on se place dans la situation c'est à J₁ de jouer.

Le déroulement de la partie peut être vu comme un arbre :

• la racine correspond à l'état actuel du jeu ;
• les nœuds à profondeur paire correspondent aux nœuds où J₁ doit jouer, à profondeur impaire les nœuds où c'est à J₂ ;
• chaque arc correspond à un coup joué et lie un état où ce coup est autorisé à l'état résultant de l'application du coup ;
• aux feuilles, nous trouvons les fins de partie : les états gagnants ou perdants pour J₁, ou encore les états bloqués (matches nuls) ;
• un chemin allant de la racine à une feuille décrit une partie possible.

On voit là un parallèle assez fort avec les graphes d'états : l'état initial est la situation actuelle, les états finaux sont les fins de partie et les opérateurs correspondent les coups légaux. Cependant il manque dans cette formalisation la présence de deux joueurs distincts et l'alternance de leurs coups. Cela qui justifie le développement d'algorithmes spécifiques.

Algorithme Min-Max

On prend la convention suivante :

• une situation gagnante pour J₁ vaut +1 ;
• une situation perdante pour J₁ vaut -1 ;
• une situation nulle vaut 0.

L'idée est de l'algorithme est de développer complètement l'arbre de jeu, de noter chaque feuille avec sa valeur, puis de faire remonter ces valeurs avec l'hypothèse que chaque joueur choisit le meilleur coup pour lui. Cela signifie en pratique que :

• J₁ choisit le coup amenant à l'état de plus grande valeur ;
• J₂ choisit le coup amenant à l'état de plus petite valeur.

On applique le principe du Min-Max Jeu de Nim à 3 allumettes (chaque joueur peut à chaque coup prendre 1, 2 ou 3 allumettes et celui qui prend la dernière allumette a perdu).

On commence par développer l'arbre de jeu :

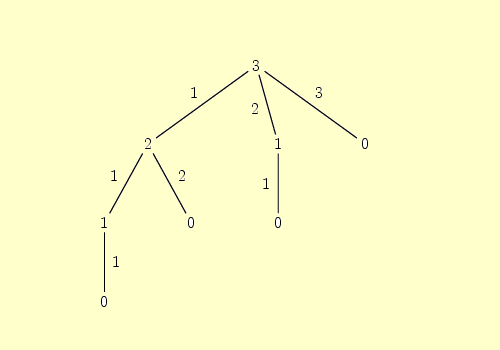
puis on étiquette les feuilles selon qu'il s'agit d'une partie gagnante ou perdante :

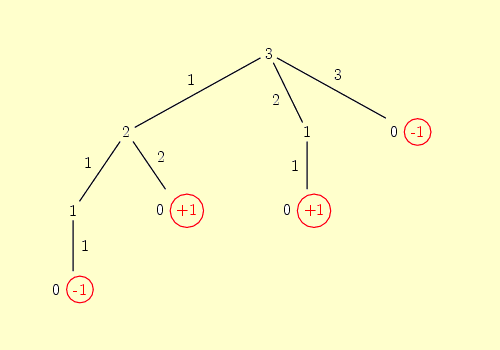
enfin, on fait remonter les évaluations depuis les feuilles jusqu'à la racine (en bleu les nœuds où l'on maximise, en vert les nœuds où l'on minimise) :

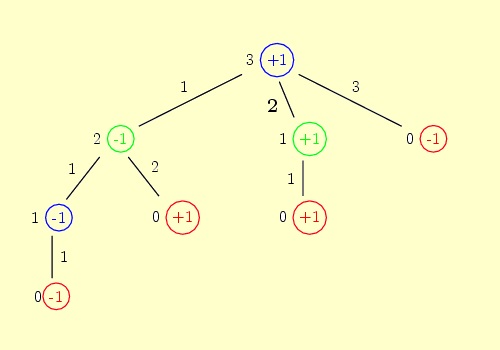
et l'on conclut que le premier joueur doit enlever deux allumettes.

Algorithme DecisionMinMax (e,J) 
{ Décide du meilleur coup à jouer par le joueur J dans la situation e }
Début
  Pour chaque coup de CoupJouables(e,J) faire
    valeur[coup] = ValeurMinMax(Applique(coup,e),J,false)
  Fin pour
  retourner (coup tel que valeur[coup] est maximale)
Fin

Algorithme ValeurMinMax (e,J,EstUnEtatMax) 
{ Calcule la valeur de e pour le joueur J selon que e EstUnEtatMax ou pas }
Début
  Si PartieGagnante(e,J) Alors retourner(+1)
  Sinon Si PartiePerdante(e,J) Alors retourner(-1)
        Sinon Si PartieNulle(e,J) Alors retourner(0)
              Sinon 
                 vals = vide
                 Pour s parmi les successeurs de e faire
                    ajouter ValeurMinMax(s,J,not(EstUnEtatMax))) à vals
                 Fin pour
                 Si EstUnEtatMax
                 Alors retourner(maximum de vals)
                 Sinon retourner(minimum de vals)
              Fin si
        Fin si
  Fin si
Fin

En pratique, l'algorithme Min-Max n'est pas utilisé en l'état : il est rarement possible de développer l'ensemble de l'arbre de jeu.

• limiter la profondeur d'exploration ;
• effectuer des coupes dans l'arbre de jeu.

Ce sont ces deux adaptations que nous détaillons ci-dessous.

Algorithme Min-Max avec profondeur bornée

Interrompre l'exploration de l'arbre avant d'avoir atteint des fins de partie implique de pouvoir évaluer l'état du jeu à un instant quelconque. Cela est rendu possible par l'utilisation d'une fonction heuristique h(e,J) qui évalue la situation e pour le joueur J.

Étant données cette fonction d'évaluation h et une profondeur maximale, l'algorithme Min-Max se modifie comme suit :

Algorithme DecisionMinMax (e,J) 
{ Décide du meilleur coup à jouer par le joueur J dans la situation e }
Début
  Pour chaque coup de CoupJouables(e,J) faire
    valeur[coup] = ValeurMinMax(Applique(coup,e),J,false)
  Fin pour
  retourner (coup tel que valeur[coup] est maximale)
Fin

Algorithme ValeurMinMax (e,J,EstUnEtatMax,pmax) 
{ Calcule la valeur de e pour le joueur J selon que e EstUnEtatMax ou pas
  et pmax la profondeur maximale }
Début
  Si PartieGagnante(e,J) Alors retourner(+ValMax)
  Sinon Si PartiePerdante(e,J) Alors retourner(-ValMax)
        Sinon Si PartieNulle(e,J) Alors retourner(0)
              Sinon 
                 Si pmax=0 Alors retourner h(s,J)
		 Sinon
                   vals = vide
                   Pour s parmi les successeurs de e faire
                      ajouter ValeurMinMax(s,J,not(EstUnEtatMax),pmax-1)) à vals
                   Fin pour
                   Si EstUnEtatMax
                   Alors retourner(maximum de vals)
                   Sinon retourner(minimum de vals)
                Fin si
              Fin si
        Fin si
  Fin si
Fin

On part d'un arbre de jeu dont la profondeur a été fixée à 4 et pour lequel on dispose des évaluations aux feuilles :

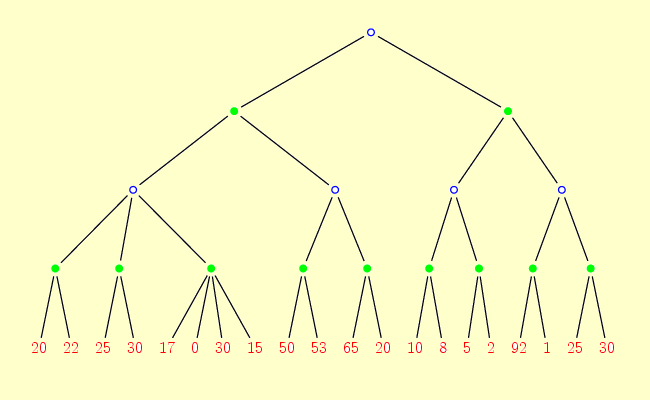
On fait remonter les valeurs selon la méthode Min-Max, ce qui nous indique le coup à jouer :

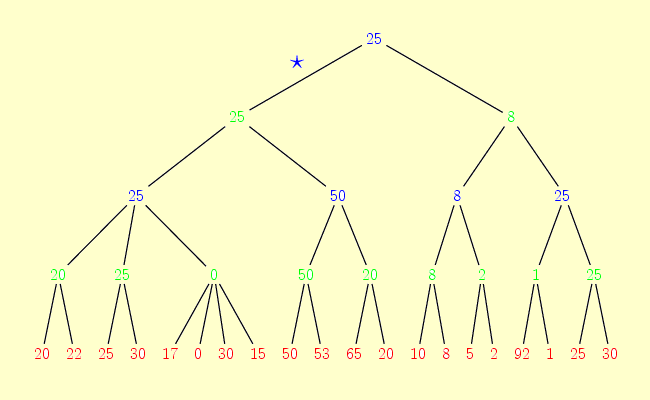
Les résultats de la méthode sont donc maintenant liés à la qualité de h et au nombre de coups d'avance que l'on autorise dans le développement de l'arbre.

h devra être redéfinie pour chaque jeu, en y incluant toute la connaissance possible.

La profondeur maximale est souvent liée à la machine utilisée mais également à l'avancement dans la partie (on peut souvent aller plus profond en fin de partie). Précisons, le niveau des joueurs artificiels d'échecs en fonction de cette profondeur limite (précisons qu'ici un coup signifie en fait un échange, l'action de J₁ et la réplique de J₂) :

• 2 coups : novice ;
• 4 coups : maître ;
• 6-7 coups : champion du monde.

Coupes Alpha et Bêta

L'idée est d'élaguer certaines branches de l'arbre. Il ne s'agit pas cependant de mettre en place une heuristique de coupure mais de couper sans risque.

On distingue deux types de coupures, alpha et bêta, illustrées ci-dessous.

Considérons l'arbre suivant dont la racine est de type MAX et développée sur deux niveaux ainsi que les premiers évalués.

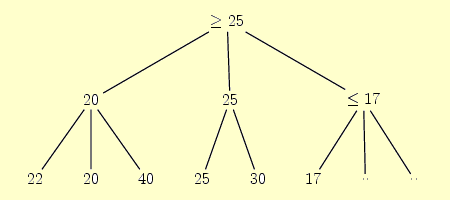
À ce stade du développement, on sait que la valeur de la racine sera supérieure ou égale à 25, en aucun cas elle ne peut être inférieure car nous sommes sur un nœud MAX. Or, il apparaît que la valeur remontée par son troisième fils sera inférieure ou égale à 17. On en déduit que la valeur de la racine ne viendra pas de cette branche et on peut se dispenser d'aller voir les derniers nœuds. Il s'agit d'une coupe alpha.

Une coupe bêta est illustrée par l'arbre suivante :

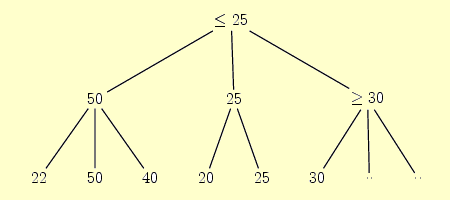
Naturellement, à l'échelle d'un arbre de jeu, cette technique peut provoquer l'élagage de sous-arbres de taille importante.

Soulignons que l'efficacité de cet élagage est directement liée à l'ordre d'évaluation des nœuds. Une amélioration est alors de classer ces nœuds suivant h, pour permettre un élagage maximal mais cela suppose que la fonction h ne soit pas trop longue à calculer.

Algorithme DecisionAlphaBeta (e,J) 
{ Décide du meilleur coup à jouer par le joueur J dans la situation e }
Début
  alpha = -ValMax
  Pour chaque coup de CoupJouables(e,J) faire
    val = ValeurAlphaBeta(Applique(coup,e),J,alpha,+MaxVal,false)
    Si (val>alpha)
    Alors
      action = coup
      alpha  = val
    Fin si 
  Fin pour
  retourner action
Fin

Algorithme ValeurAlphaBeta (e,J,alpha,beta,EstUnEtatMax,pmax) 
{ Calcule la valeur de e pour le joueur J selon que e EstUnEtatMax ou pas
  et pmax la profondeur maximale }
Début
  Si PartieGagnante(e,J) Alors retourner(+ValMax)
  Sinon Si PartiePerdante(e,J) Alors retourner(-ValMax)
        Sinon Si PartieNulle(e,J) Alors retourner(0)
              Sinon 
                 Si pmax=0 Alors retourner h(s,J)
		 Sinon
                   Si EstUnEtatMax
                     Pour s parmi les successeurs de e faire
                        alpha = MAX(alpha,ValeurAlphaBeta(s,J,alpha,beta,not(EstUnEtatMax),pmax-1)
                        Si alpha >= beta
                        Alors retourner(alpha) /* coupe beta */
                        Fin si 
                     Fin pour
                     retourner(alpha)
                   Sinon
                     Pour s parmi les successeurs de e faire
                        beta = MIN(beta,ValeurAlphaBeta(s,J,alpha,beta,not(EstUnEtatMax),pmax-1)
                        Si beta <= alpha
                        Alors retourner(beta) /* coupe alpha */
                        Fin si 
                     Fin pour
                     retourner(beta)
                   Fin si
                Fin si
         Fin si
  Fin si
Fin

Autres optimisations

Il est un peu ridicule de lancer une exploration dès le début de la partie, d'autant plus qu'elle ne pourra se faire qu'à une profondeur très limitée à ce stade de la partie. C'est pourquoi il est classique de calculer les premiers coups à l'avance, avec une profondeur de recherche élevée. Cela est comparable aux ouvertures apprises par cœur par les joueurs humains.

De la même manière, on peut se constituer une bibliothèque de fins de partie : c'est bien sûr un moment critique où il faudrait jouer parfaitement, autrement dit développer l'arbre de jeu jusqu'aux fins de partie et cela, le plus tôt possible. Encore une fois, ces calculs peuvent être faits à l'avance et les résultats stockés.

Une autre optimisation est de faire varier la profondeur de recherche selon le moment ou l'état de la partie, autrement dit aller plus profond lorsque :

• lorsqu'il n'y a pas beaucoup de coups possibles et que l'on peut donc explorer plus profond dans le temps imparti ;
• lorsque les situations évaluées aux feuilles semblent instables et qu'il faut poursuivre un peu pour déterminer qui a vraiment l'avantage ;
• uniquement pour le coup qui a été choisi et dans le but de confirmer ce choix (il s'agit là de combattre l'effet d'horizon, défaut connu des algorithmes de type Min-Max) ;
• en fin de partie.

Confrontations machines vs humains

Puissance 4

Le jeu est résolu. Cela signifie que l'on a montré qu'il existait une stratégie gagnante pour le joueur qui commence à jouer. Cette stratégie étant stockée dans une base de données, il est facile pour un joueur artificiel de suivre cette stratégie et de gagner systématiquement.

Othello

Pour ce jeu, il n'y a pas de confrontation entre joueurs humains et joueurs artificiels. Il est clair que les joueurs artificiels sont supérieurs.

Les dames

Le programme Chinook basé sur un alpha-bêta est devenu champion des États-Unis en 1992, puis champion du monde en 1994. Ce joueur utilise également une bibliothèque de fins de partie (tous les damiers comportant 8 pièces ou moins).

Les échecs

DeepBlue bat Kasparov en 1997. Depuis, toutes les confrontations tournent systématiquement à l'avantage de la machine. Utilisation de l'algorithme alpha-bêta, le facteur de branchement vaut ici 40.

Le Go

Le facteur de branchement au Go est de 360. En 2015, 2016 et 2017, le programme AlphaGo a enchaîné les victoires contre des joueurs professionnels.

Comment joue le joueur humain ?

On ne connaît pas tous les mécanismes mis en jeu dans un cerveau humain lors d'une partie mais différentes études démontrent que son fonctionnement est très éloigné des algorithmes que nous avons présentés.

On a vu qu'en moyenne, il y avait 40 coups possibles à jouer aux échecs, 40 possibilités que nos algorithmes sont dans l'obligation de considérer. Or, des expériences de poursuite visuelle (observation du mouvement des yeux) chez le champion humain montrent que celui-ci se concentre uniquement sur 4 ou 5 coups parmi les 40 possibles.

Dans une autre expérience, on montre très rapidement des échiquiers à un champion, puis on lui demande ceux qui ressemblent le plus à un échiquier donné. Le résultat est très contre-intuitif, en particulier pour un novice : les échiquiers choisis semblent souvent très différents, même s'ils peuvent correspondre à des situations de jeu comparables. La conclusion de cette expérience est que la représentation interne d'un échiquier chez le champion d'échecs n'est sûrement pas une matrice 8x8 mais une structure qui met en avant les zones sensibles de l'échiquier.

Finalement, il apparaît que les zones du cerveau activées pendant une partie d'échecs sont liées à la représentation spatiale, plutôt qu'à la réflexion pure.