Pense-bêtes en Statistiques
Des carrés dans la formule de l'écart-type ?
J'ai toujours trouvé bizarre la formule de l'écart-type :
pourquoi utiliser les carrés des observations
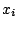 ?
L'âge du capitaine au carré, ça n'a pas sens.
Du coup, on est obligé ensuite de prendre la racine carrée
pour retrouver un résultat qui respecte l'unité des observations.
?
L'âge du capitaine au carré, ça n'a pas sens.
Du coup, on est obligé ensuite de prendre la racine carrée
pour retrouver un résultat qui respecte l'unité des observations.
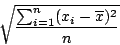
On pourrait utiliser l'écart absolu moyen :
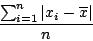
Il faut revenir à la base : nous avons un ensemble d'observations
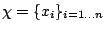 et nous voulons déterminer pour cet ensemble une valeur centrale
et nous voulons déterminer pour cet ensemble une valeur centrale
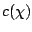 et une dispersion
et une dispersion 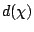 autour de cette valeur centrale.
autour de cette valeur centrale.
Supposons la dispersion calculée par la formule :
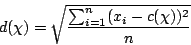
Assez logiquement, on voudrait que, pour des
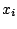 fixés,
le choix de
fixés,
le choix de 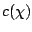 minimise la dispersion
minimise la dispersion 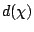 .
On cherche donc la valeur de
.
On cherche donc la valeur de 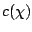 qui annule la dérivée de
qui annule la dérivée de 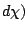 :
:
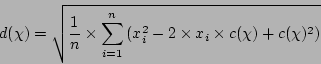
donc
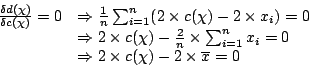
et par conséquent :
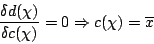
Ainsi, c'est le choix de l'écart-type comme mesure de dispersion qui amène à choisir la moyenne comme valeur centrale.
Menons le même raisonnement avec comme mesure de dispersion :
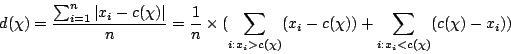
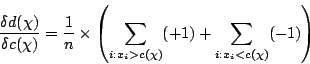
Pour annuler cette dérivée, il faut choisir la valeur centrale
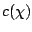 de telle manière que exactement la moitié des
de telle manière que exactement la moitié des
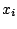 lui soient supérieurs et les autres inférieurs. C'est la définition de la médiane.
lui soient supérieurs et les autres inférieurs. C'est la définition de la médiane.
En conclusion, plus que sur la mesure de dispersion elle-même, le choix porte sur un couple (valeur centrale,mesure de dispersion) : (moyenne,écart-type) ou (médiane,écart-absolu-moyen).
Calculer la moyenne et l'écart-type en même temps
La formule classique de la variance oblige à disposer de la moyenne. Il est cependant possible de calculer les deux en même temps : il suffit de faire simultanément la somme des valeurs observées et la somme de leurs carrés.
s = 0;
s2 = 0;
for i=1 to n do begin
s = s + x[i];
s2 = s2 + x[i]*x[i];
end;
moyenne = s/n;
variance = s2/n - moyenne*moyenne;
ecart = racine(variance);
La démonstration est laissée au lecteur (c'est facile !).
Corrélation des rangs entre deux ordres
Nous présentons deux méthodes classiques pour déterminer la corrélation des rangs entre deux ordres :
- le coefficient de corrélation des rangs de Spearman ;
- le coefficient de corrélation des rangs de M. G. Kendall.
Les brèves descriptions qui suivent sont tirées de
Probabilités, Analyse de Données et Statistique,
G. Saporta,
Chapitre 7, pages 141 à 145.
Une implémentation commode est fournie avec le langage R.
Précisons immédiatement que ces deux coefficients varient entre -1 (les deux classements sont inversés l'un par rapport à l'autre) et 1 (les classements sont identiques), en passant par 0 (les classements sont indépendants).
Dans la suite, on considère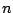 objets
objets
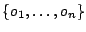 pour lesquels on dispose de deux classements
pour lesquels on dispose de deux classements
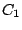 et
et
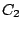 .
On notera
.
On notera
![$C_{1}[o_{i}]$](/divers/statistiques/Images/img5.png) et
et
![$C_{2}[o_{i}]$](/divers/statistiques/Images/img6.png) les positions de l'objet
les positions de l'objet
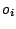 dans les deux classements.
dans les deux classements.
Le coefficient de corrélation des rangs de Spearman
Ici, on compare pour chaque objet ses rangs dans les deux classements :
Pour savoir si la valeur trouvée est significative, on se reporte à la table du coefficient de Spearman.
Le coefficient de corrélation des rangs de M. G. Kendall
Cette fois, on compte le nombre de couples
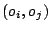 pour lesquels les deux classements s'accordent sur le fait que
pour lesquels les deux classements s'accordent sur le fait que
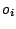 est avant
est avant
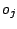 .
Soit
.
Soit
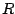 ce nombre.
ce nombre.
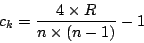
Pour savoir si la valeur trouvée est significative, on utilise
que la distribution de
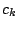 est approximable par une loi de Laplace-Gauss (approximation satisfaisante dès que
est approximable par une loi de Laplace-Gauss (approximation satisfaisante dès que
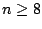 ) :
) :