Technique de bagging (Léo Breiman, 1996)
Compromis biais-variance
L'erreur en généralisation peut être décomposée en deux termes : biais et variance.
Ces deux types d'erreur sont liées au langage choisi.
- Soit celui-ci est trop pauvre pour contenir le concept cible et, dans ce cas, l'apprentissage revient à chercher la meilleure approximation de la cible dans le langage. L'erreur de l'approximation finalement trouvée sera due au biais (de langage).
- Soit le concept cible peut être représenté dans le langage des hypothèses mais, cette fois, la richesse du langage fait qu'il est probable que d'autres hypothèses aient le même comportement que la cible sur les données disponibles. L'algorithme d'apprentissage doit choisir parmi ces candidats équivalents, au hasard. L'erreur en généralisation de l'hypothèse choisie sera due à la variance.
Ces deux objectifs, réduire la variance et réduire le biais, sont naturellement incompatibles et c'est le meilleur compromis qui doit être trouvé.
Algorithmes de base
Cette technique concerne les apprenants dont l'erreur est due en plus grande partie à la variance, c'est-à-dire des apprenants qui réagissent à de petites modifications de l'ensemble d'apprentissage en produisant des hypothèses différentes à chaque fois.
La solution proposée est justement d'utiliser plusieurs fois l'appenant pour obtenir autant d''hypothèses et les combiner au sein d'un vote. Pour obtenir des hypothèses différentes, le bagging propose de construire de nouveaux échantillons à partir des données initiales.
Échantillonnage
- Entrée :
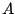 un ensemble des données d'apprentissage contenant
un ensemble des données d'apprentissage contenant
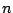 exemples ;
exemples ;
- Sortie :
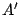 un nouvel ensemble de données de même taille ;
un nouvel ensemble de données de même taille ;
- Tirer avec remise
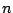 exemples de
exemples de 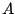 et les placer dans
et les placer dans 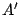 .
.
Bagging
- Entrées : un ensemble d'exemples
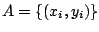 , un nombre d'itérations
, un nombre d'itérations 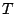 à effectuer, un apprenant
à effectuer, un apprenant 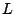 ;
;
- Sortie :
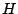 le classifieur final ;
le classifieur final ;
- Pour
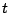 allant de 1 à
allant de 1 à 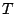
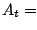 Échantillonnage(
Échantillonnage(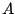 )
)
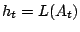
- retourner
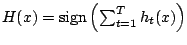
La technique a été pensée pour les apprenants instables mais il est ensuite naturel de vouloir l'utiliser pour les apprenants dont nous disposons. Si ces algoritmes sont naturellement stables, on les rend instables, le plus souvent en ajoutant du stochastique !
Bagging d'arbres
Léo Breiman a ensuite proposé du bagging d'arbres de décision. Les méthodes comme C4.5 étant plutôt stables, il faut ajouter du stochastique dans la construction de l'arbre.
Il y a plusieurs manières de faire cela. Celle retenue ici est de ne considérer qu'un sous-ensemble des
attributs à chaque nœud de l'arbre. Ces sous-ensembles sont construits par un tirage aléatoire
uniforme de 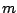 attributs parmi tous ceux disponibles. Le test choisi a un nœud est le meilleur
selon un critère entropique classique parmi tous les tests que l'on peut contruire sur les
attributs parmi tous ceux disponibles. Le test choisi a un nœud est le meilleur
selon un critère entropique classique parmi tous les tests que l'on peut contruire sur les 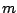 variables sélectionnées.
variables sélectionnées.
Cette méthode nécessite donc le règlage du paramètre 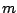 .
.
Adaboost
Introduction
On a vu que l'algorithme adaboost nous venait du cadre PAC.
Adaboost
- Entrées :
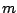 exemples
exemples  et leurs classes
et leurs classes 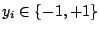 ;
; 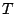 un nombre d'itérations à effectuer ;
un nombre d'itérations à effectuer ; 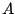 un apprenant faible acceptant en entrée un échantillon d'exemples étiquetés et pondérés.
un apprenant faible acceptant en entrée un échantillon d'exemples étiquetés et pondérés.
- Sortie :
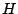 le classifieur final.
le classifieur final.
- Pour
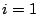 à
à 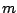 :
: 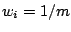 initialisation des poids des exemples
initialisation des poids des exemples
- Pour
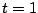 à
à 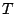
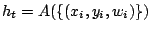
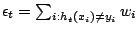
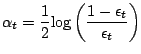
![$\displaystyle Z_{t} = \sum_{i=1}^{m} \left[ w_{i}.\mbox{exp}(-\alpha_{t} y_{i} h_{t}(x_{i})) \right]$](/Enseignement/Cours/Apprentissage-Automatique/combinaisons/img22.png)
- Pour
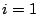 à
à 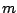 :
: 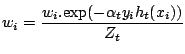
- return
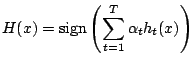
Voir l'applet de Yoav Freund montrant le comportement d'AdaBoost.
Dans le cadre PAC, des conditions ont été définies pour que Adaboost produise un boosting effectif et dans la pratique nous devons donc nous interroger sur les points suivants :
- dispose-t-on d'assez d'exemples ?
- le nombre d'itérations dans Adaboost est-il suffisant ?
- l'apprenant utilisé est-il réellement faible au sens du modèle PAC, c'est-à-dire est-il meilleur qu'un classifieur aléatoire quelle que soit la distribution ?
A priori, on ne peut pas intervenir sur le premier point : il faut faire avec les exemples dont nous disposons, difficile d'en inventer d'autres. Le nombre d'itérations peut être augmenté si l'on a du temps et avec le risque d'un sur-apprentissage. Enfin, il est difficile de montrer qu'un apprenant fournit toujours des hypothèses meilleures que le hasard mais les candidats sont nombreux : arbres de décision limités à un niveau (decision stumps), arbres de décision, réseaux de neurones, classifieurs naïfs, etc.
Malgré ces inconnues, les résultats rapportés pour Adaboost sont très bons. Des propositions ont donc été émises pour expliquer ces bons résultats et tenter de les améliorer encore.
Compromis biais/variance
Léo Breiman a essayé de reprendre l'explication des performances du bagging pour justifier celles du boosting, à savoir la diminution de l'erreur due à la variance. Il considère que ces deux méthodes appartiennent à une même famille, les arcing classifiers (Adaptively Resample and Combine).
Il est cependant apparu que le boosting faisant plus que diminuer l'erreur due à la variance et qu'expérimentalement le boosting obtenait de meilleurs résultats que le bagging.
Minimiser l'erreur empirique
On a l'inégalité suivante :
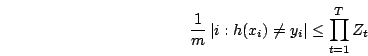
Une stratégie possible est alors d'essayer de minimiser chacun des 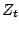 .
Cette piste conduit à :
.
Cette piste conduit à :
- contraindre l'apprenant à fournir à chaque étape
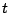 l'hypothèse
qui minimise
l'hypothèse
qui minimise 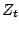 ;
;
- définir
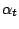 comme suit :
comme suit :

avec

Prise en compte des marges
Une observation est souvent rapportée au sujet d'Adaboost : l'erreur en généralisation continue à chuter alors que l'erreur empirique ne varie plus (parfois elle est simplement nulle). La première leçon de cette observation est que la stabilisation de l'erreur empirique n'est pas un bon critère d'arrêt.
Une explication possible à cette observation passe par les marges. La marge d'un exemple est défini par :

Autrement dit, il s'agit de la somme des votes exprimés sur cet exemple par les hypothèses produites, chacune votant avec son poids normalisé.
Un exemple pour lequel toutes les hypothèses s'accorderaient sur la même classe aurait donc une marge de 1. Intuitivement, on aurait plus confiance dans cette classification que dans le même prédiction avec une marge de seulement 0.1.
Il existe une inégalité qui confirme cette intuition et que voici dans une forme simplifiée : pour tout 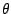 , on a
, on a
![\begin{displaymath}
\mbox{erreur}(H) = P[y_{i}.f(x_{i}) \leq 0] \leq P[y_{i}.m(x...
...left( \sqrt\frac{log \vert{\cal C}\vert}{m.\theta^{2}} \right)
\end{displaymath}](/Enseignement/Cours/Apprentissage-Automatique/combinaisons/img32.png)
Expérimentalement, on constate effectivement que Adaboost fait croître les marges, même après que l'erreur empirique ne baisse plus, ce qui explique le phénomène observé.
Cependant, on peut vérifier qu'AdaBoost ne produit pas les marges maximales, ce qui semble laisser la porte ouverte à une éventuelle optimisation.
À nouveau les résultats sont négatifs :
- les modifications d'Adaboost visant à optimiser explicitement la marge n'entraînent pas d'amélioration sur les prédictions ;
- Michael Harries démontre qu'un algoritme qui fait voter des arbres parfaits (tous les exemples d'apprentissage ont donc une marge maximale de 1) n'a pas de meilleurs résultats que Adaboost.
Productions stochastiques d'hypothèses
Tom Dietterich comparent systématiquement les performances d'arbres de décision appris par bagging, boosting, ou produits de manière stochastique.
Pour la production stochastique, la stratégie suivante est adoptée : à chaque nœud, tous les tests possibles sont considérés, évalués et classés, puis le test associé au nœud est choisi parmi les 20 meilleurs.
Les hypothèses produites par les trois méthodes sont comparées suivant deux critères : leur taux d'erreur et leur diversité. Il apparaît alors que le bagging et la production stochastique fournissent des hypothèses assez semblables et de faible erreur. Par contre, Adaboost produit des hypothèses beaucoup plus diverses, dont certaines avec des taux d'erreur élevés.
Les expérimentations menées par Tom Dietterich amènent aux conclusions suivantes :
- le bagging nécessite beaucoup d'exemples ;
- en l'absence de bruit : adaboost > stochastique > bagging ;
- en présence de bruit : bagging > stochastique > adaboost.
Lectures
Autour de AdaBoost
Experiments with a New Boosting Algorithm
ICML 1996, pages 148-156.
[ page CiteSeer ]
Autres techniques
Bagging Predictors
Machine Learning Journal, 24:2, pages 123-140, 1996.
[ page CiteSeer ]
An Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting, and Randomization
Machine Learning Journal, 40:2, pages 139--158, 2000.
[ page CiteSeer ][ postscript gzippé ]
Ensemble Methods in Machine Learning
First International Workshop on Multiple Classifier Systems, LNCS 1857, pages 1-15, 2000.
[ page CiteSeer ][ postscript gzippé ]
Explications théoriques
Monte Carlo Theory as an Explanation of Bagging and Boosting
IJCAI 2003, pages = 499-504.
[ version PDF ]
