Moindres généralisés
- Supports 2009-2010 (slides en PDF, 1 ou 4 ou 8 slides par page) : (1on1)(4on1)(8on1)
- Démonstrateur « apprentissage de combinaisons à base de moindres généralisés »
Introduction aux moindres généralisés
Comme son nom l'indique, le moindre généralisé de deux exemples est l'hypothèse la plus spécifique possible qui couvre ces deux exemples. En attribut-valeur, cette hypothèse est unique et peut être simplement définie comme suit :
- si les deux exemples partagent la même valeur d'un attribut catégoriel, celle-ci est conservée dans le moindre généralisé ; si ces valeurs sont distinctes, le moindre généralisé fait apparaître une valeur indéterminée pour cet attribut ;
- pour un attribut continu, on construit le plus petit intervalle incluant les deux valeurs présentes dans les exemples à généraliser.
Cette procédure apparaît clairement sur l'exemple suivant :
| âge | fumeur | sexe | classe | |
|---|---|---|---|---|
| e1 | 25 | non | homme | positif |
| e2 | 35 | non | femme | positif |
| g1 | [25,35] | non | ? | positif |
Naturellement, cette opération peut se généraliser pour s'appliquer à deux hypothèses ou, cas qui nous intéresse le plus, à une hypothèse et un exemple :
| âge | fumeur | sexe | classe | |
|---|---|---|---|---|
| g1 | [25,35] | non | ? | positif |
| e3 | 30 | oui | homme | positif |
| g2 | [25,35] | ? | ? | positif |
| e4 | 40 | non | femme | positif |
| g3 | [25,40] | ? | ? | positif |
Du point de vue de l'apprentissage supervisé, il est intéressant de généraliser ensemble des exemples d'une même classe, en prenant garde à ne pas couvrir d'exemples d'autres classes. Ce calcul fournit la caractérisation d'un sous-concept au sein d'une classe comme l'illustre cet exemple basé sur le problème du morpion (ou tic-tac-toe) :
|
|
->(moindre généralisé) -> |
|
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
| v (moindre généralisé) v | ||||||||||||||||||||||||||||||
|
-> (subsume) -> |
|
||||||||||||||||||||||||||||
Le résultat produit s'appelle un moindre généralisé maximalement correct et son calcul est décrit formellement par l'algorithme suivant (étant donné un exemple-graine, on essaye de généraliser, un à un, les exemples de la même classe avec comme critère d'acceptation, la correction, c'est-à-dire la non couverture d'exemples d'autres classes) :
MG_Correct_v1
- Entrées :
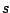 un exemple graine,
un exemple graine,
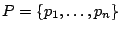 un ensemble ordonné
de
un ensemble ordonné
de 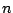 exemples de la même classe que la graine,
exemples de la même classe que la graine,
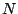 un ensemble de contre exemples.
un ensemble de contre exemples.
- Sortie :
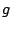 une généralisation de
une généralisation de
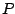 , maximalement correcte par rapport à
, maximalement correcte par rapport à
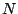 .
.
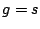
- Pour
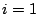 à
à 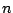
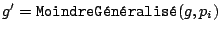
- Si not(
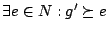 )
alors
)
alors 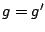 [ si
[ si 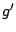 est correcte, elle devient la généralisation courante.]
est correcte, elle devient la généralisation courante.]
- retourner
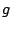
La généralisation produite est maximalement correcte dans le sens où plus aucun exemple d'apprentissage ne peut lui être ajoutée sans perdre la correction. Notons également que cette hypothèse est fonction de l'ordre dans lequel les exemples sont testés pour l'ajout.
L'exemple suivant montre trois exécutions possibles de l'algorithme précédent (les exemples qui provoquent une perte de correction pour la généralisation courante sont soulignés) :
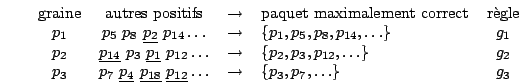
On y voit l'importance de l'ordre de présentation des exemples et également que la contrainte de correction amène des généralisations qui prisent isolément ne couvrent pas tous les exemples positifs. Autrement dit, une telle généralisation ne peut conclure que sur une seule classe, la classe des exemples sur lesquels elle a été construite. Pour tous les autres exemples, ceux de la même classe qui ne sont pas couverts et ceux d'autres classes, la généralisation ne fournit pas de classe, elle s'abstient.
L'algorithme GloBo
Évidemment, à moins qu'il y ait une solution conjonctive dans le langage des hypothèses,
le résultat dépend de l'ordre de présentation des exemples :
plusieurs règles maximalement correctes peuvent être obtenus à
partir d'une même graine 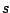 , mais en utilisant des ordres différents
des exemples de la même classe.
, mais en utilisant des ordres différents
des exemples de la même classe.
Pour compenser la dépendance vis-à-vis de l'ordre des exemples, GloBo va construire une régle maximalement correcte pour chaque exemple positif : chacun étant tour à tour utilisé comme graine et les autres exemples positifs étant présentés dans des ordres différents à chaque fois (ces listes sont mélangées aléatoirement).
Puisque nous construisons une règle pour chaque exemple positif, un sous-concept peut apparaître à chaque fois que l'on utilise un exemple de ce sous-concept comme graine.
Parmi toutes les règles obtenues, GloBo choisit ensuite les plus intéressantes en construisant une couverture des exemples positifs par un nombre minimal de règles. Ce problème est NP-difficile et c'est pourquoi nous utilisons l'heuristique qui consiste à privilégier les règles de plus grande taille.
couverture minimale approchée
Étant donnés 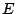 l'ensemble à couvrir et
l'ensemble à couvrir et
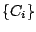 les sous-ensembles candidats.
les sous-ensembles candidats.
- Soient noncouverts =
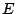 et solution =
et solution = 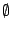 .
.
- Tant que noncouverts
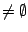 Faire
Faire
- Soit
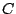 le sous-ensemble qui a la plus grande intersection avec noncouverts.
le sous-ensemble qui a la plus grande intersection avec noncouverts.
- Les éléments de
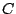 sont effacés de noncouverts
et
sont effacés de noncouverts
et 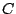 est ajouté à la solution.
est ajouté à la solution.
- Soit
- Retourner solution.
Le résultat de cet algorithme est montré sur la figure suivante :
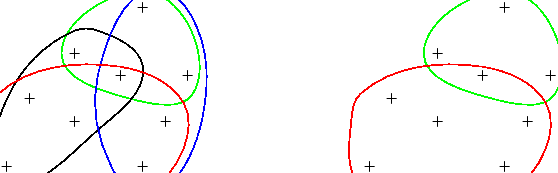
Comme tous les exemples positifs ont successivement été utilisés comme graine, il s'ensuit que la réunion des règles couvre cet ensemble d'exemples. Par suite, il existe une couverture des exemples positifs par les règles produites et cet algorithme va terminer.
Une couverture minimale approchée d'un ensemble de taille
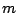 par
par 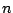 ensembles, en utilisant cette méthode, a une complexité en
ensembles, en utilisant cette méthode, a une complexité en
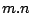 .
Ainsi, GloBo trouvera une couverture des exemples positifs
avec une complexité au pire en
.
Ainsi, GloBo trouvera une couverture des exemples positifs
avec une complexité au pire en
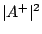 .
.
L'algorithme principal de GloBo est finalement le suivant :
GloBo
- Entrées :
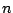 exemples
exemples
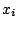 et leurs classes
et leurs classes
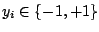 .
.
- Sortie :
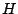 un ensemble de règles.
un ensemble de règles.
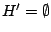
- Pour
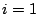 à
à 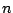
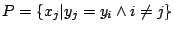
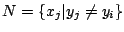
- mélanger
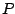 aléatoirement
aléatoirement
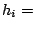 MG_Correct_v1
(
MG_Correct_v1
(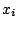 ,
,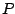 ,
,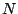 )
)
- ajouter
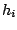 à
à 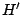
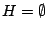
- Tant que
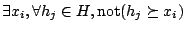
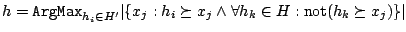
- ajouter
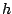 à
à 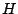
- retourner
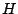
Booster des moindres généralisés
Méthode
Nous proposons ici une nouvelle version du calcul de moindres généralisés corrects destinée à devenir un apprenant faible pour AdaBoost. Cela implique de prendre en compte les poids des exemples, autrement dit de favoriser la couverture des exemples de poids élevé. Avec cet objectif, l'idée de notre apprenant faible est de réutiliser notre premier algorithme en triant au préalable les exemples candidats à la généralisation par poids décroissants. Précisons immédiatement que, quels que soient les poids, nous ne relâchons pas notre critère de correction : la généralisation produite ne couvrira aucun contre-exemple, même de poids faible. Cette nouvelle version est présentée par l'algorithme suivant :
MG_Correct_v2 (apprenant faible)
- Entrées :
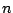 exemples
exemples
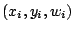 avec leurs étiquettes
et poids.
avec leurs étiquettes
et poids.
- Sortie :
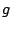 une généralisation maximalement correcte d'exemples de poids élevés.
une généralisation maximalement correcte d'exemples de poids élevés.
- target = classe choisie au hasard
- seed = l'exemple de la classe target ayant le poids le plus fort
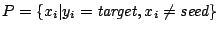
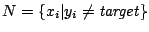
- trier
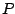 par poids décroissants
par poids décroissants
- retourner MG_Correct_v1(seed,
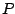 ,
,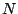 )
)
Cet apprenant est ensuite fourni à une version modifiée d'AdaBoost capable de gérer les hypothèses qui s'abstiennent. Cette version définit pour chaque hypothèse trois quantités :
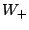 la somme des poids des exemples bien classés ;
la somme des poids des exemples bien classés ;
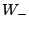 la somme des poids des exemples mal classés ;
la somme des poids des exemples mal classés ;
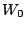 la somme des poids des exemples sur lesquels l'hypothèse s'abstient.
la somme des poids des exemples sur lesquels l'hypothèse s'abstient.
Et définit le poids d'une hypothèse comme :
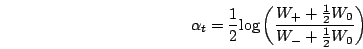
Remarquons que cette formule se simplifie en prenant en compte que les moindres généralisés
ainsi calculés ne font pas d'erreur de classification (ils classifient bien ou s'abstiennent).
En effet, 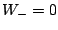 et par suite
et par suite
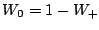 et finalement :
et finalement :

Cette instanciation de AdaBoost est dans la suite notée AdaBoostMG.
Résultats expérimentaux
Notre version d'AdaBoost a été comparée aux algorithmes suivants :
- le classique C4.5 ;
- GloBo, système à base de moindres généralisés mais sans boosting présenté précédemment ;
- AdaBoost utilisant comme apprenant faible des decision stumps (arbres de décision limités à un seul niveau), noté dans la suite AdaBoostDS.
Ces systèmes sont évalués sur vingt problèmes classiques de l'UCI représentant un éventail assez large des problèmes que l'on peut rencontrer : attributs tous continus, tous discrets, ou mélange des deux types, avec deux classes à prédire ou plus, avec ou sans valeurs manquantes, hautement disjonctif ou pas.
Pour chacun de ces problèmes, on utilise une validation croisée 10 fois, le découpage étant le même pour toutes les expérimentations. Finalement, pour chaque problème et pour chaque système, on mesure le taux d'erreur moyen sur les 10 blocs de test. Précisons que les systèmes stochastiques (GloBo et AdaBoostMG) sont exécutés dix fois sur chaque bloc et c'est la moyenne sur ces dix exécutions qui est utilisée pour mesurer l'erreur du système.
Pour 100 étapes de boosting, les résultats sont les suivants :
- les systèmes à base d'arbres de décision (C4.5 et AdaBoostDS) obtiennent les meilleurs résultats ;
- AdaBoostMG surpasse GloBo sur 14 des 20 problèmes étudiés.
Pour 1000 étapes de boosting, les résultats sont les suivants :
- l'erreur de AdaBoostMG diminue notablement sur quasiment tous les problèmes lorsque l'on passe de 100 étapes de boosting à 1000 (l'erreur globale chute de 18.16 % à 12.70 %) ;
- AdaBoostMG surpasse ou égale C4.5 sur 14 problèmes sur 20 et cette supériorité est aussi apparente sur les taux d'erreur moyens (12.70 % contre 16.18 %) ;
- GloBo est battu sur tous les problèmes par AdaBoostMG et l'on mesure ainsi ce que nous avons gagné en abandonnant la compréhensibilité des théories produites par GloBo (en moyenne, on passe de 16.31 % d'erreurs à 12.70 %) ;
- AdaBoostDS supporte moins bien que AdaBoostMG le passage à 1000 étapes de boosting et tous les indicateurs de performance se détériorent par rapport aux résultats précédents ; que ce soit avec 100 ou 1000 étapes de boosting, AdaBoostDS est maintenant battu par AdaBoostMG utilisant 1000 étapes de boosting.
Ces résultats nous encouragent à augmenter encore le nombre d'étapes de boosting pour continuer à faire baisser l'erreur. Malheureusement, le calcul de moindres généralisés corrects est coûteux : pour chacun, il faut essayer d'ajouter les exemples de la classe cible un à un et chacun de ces ajouts doit être validé sur l'ensemble des contre-exemples.
Il est donc impératif, pour que la méthode soit viable, de rendre l'apprentissage plus rapide. Avec cet objevtif, nous explorons maintenant la parallélisation de la génération des hypothèses et donc le report de l'affectation de poids à ces hypothèses.
Produire et combiner des moindres généralisés sans AdaBoost
Nous l'avons vu, la production d'un moindre généralisé correct est de complexité quadratique dans le nombre d'exemples disponibles et cela n'est pas acceptable pour un apprenant faible destiné à être appelé de nombreuses fois dans un algorithme de type AdaBoost.
Nous aurions pu, pour réduire le temps de calcul, échantillonner et distribuer les données à différentes unités de calcul. Nous avons préféré distribuer, non pas les données, mais le calcul des hypothèses, lequel se fera toujours sur l'ensemble complet des données disponibles. Cela nécessite de savoir :
- produire les hypothèses indépendamment les unes des autres ;
- affecter un poids à chacune de ces hypothèses a posteriori.
Nous commençons par le deuxième point en attribuant de nouveaux poids aux hypothèses disponibles, quel que soit leur mode de production.
Affectation de poids aux hypothèses produites
Le premier de ces poids, dans la suite repéré par le nom
adalike, cherche à imiter le mode de calcul des poids d'AdaBoost.
Comme AdaBoost, nous commençons par définir le poids d'un exemple
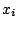 , cela à partir de
, cela à partir de
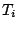 le nombre de fois où cet exemple est couvert
par les hypothèses produites :
le nombre de fois où cet exemple est couvert
par les hypothèses produites :

Cette formule fait référence à AdaBoost qui multiplie
le poids d'un exemple par
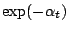 pour chaque hypothèse
pour chaque hypothèse
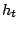 couvrant l'exemple.
Une fois ces poids attribués aux exemples, on les normalise en divisant
chacun par
couvrant l'exemple.
Une fois ces poids attribués aux exemples, on les normalise en divisant
chacun par
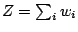 .
Puis nous définissons le poids d'une hypothèse
.
Puis nous définissons le poids d'une hypothèse
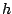 .
.
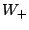 est défini comme la somme des poids des exemples couverts par
est défini comme la somme des poids des exemples couverts par
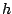 et
et 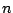 est le nombre de fois où cette hypothèse est apparue pendant la production.
Finalement, le poids adalike de
est le nombre de fois où cette hypothèse est apparue pendant la production.
Finalement, le poids adalike de
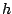 est calculé comme suit :
est calculé comme suit :
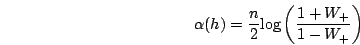
La valeur de 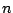 intervient pour simuler le cumul des poids effectué par AdaBoost
lorsqu'une même hypothèse apparaît plusieurs fois.
intervient pour simuler le cumul des poids effectué par AdaBoost
lorsqu'une même hypothèse apparaît plusieurs fois.
Nous considérons également les poids suivants, plus simples :
- covering : chaque hypothèse distincte vote avec un poids qui correspond au nombre d'exemples qu'elle couvre dans l'ensemble d'apprentissage (dans notre cas, les hypothèses sont correctes par construction et les exemples couverts par une hypothèse sont donc tous de la même classe) ;
- frequency : chaque hypothèse distincte vote avec un poids qui correspond à son nombre d'apparitions pendant la phase de production ;
- uniform : toutes les hypothèses distinctes votent avec un poids égal.
Production d'hypothèses sans AdaBoost
L'étape suivante est de trouver une alternative à AdaBoost pour produire des hypothèses. Nous proposons pour cela l'algorithme GloBoost : celui-ci produit des moindres généralisés corrects de façon purement stochastique et, par conséquent, sans aucun lien de dépendance entre eux. Cela nous permettra à terme de partager ce travail de génération entre plusieurs machines.
GloBoost
- Entrées :
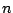 exemples
exemples
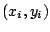 avec étiquettes ;
avec étiquettes ;
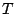 un nombre d'itérations.
un nombre d'itérations.
- Sortie :
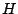 le classifieur final.
le classifieur final.
- Pour
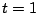 à
à
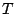
- target = classe choisie au hasard
- seed = un exemple de la classe target choisi au hasard
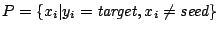
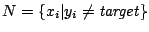
- mélanger
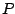 aléatoirement
aléatoirement
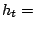 MG_Correct_v1(seed,
MG_Correct_v1(seed,
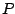 ,
,
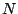 )
)
- pour tout
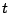 tel que
tel que
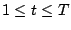 :
:
 fonction à instancier
fonction à instancier
- retourner
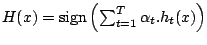
Évaluation expérimentale des poids proposés
Dans un premier temps, nous conservons l'algorithme AdaBoostMG comme générateur d'hypothèses. Après la phase de boosting, nous obtenons un ensemble d'hypothèses avec leurs poids attribués par AdaBoost et nous leurs affectons les poids supplémentaires définis précédemment. On obtient ainsi des systèmes de vote distincts même si tous sont fondés sur les mêmes votants.
Notre intuition, forgée par les différents travaux qui cherchent à redéfinir les poids pour maximiser la marge est que AdaBoost a un comportement quasi optimal dans le réglage des poids des hypothèses. Il s'agit donc ici de quantifier ce que nous perdons en abandonnant les poids des hypothèses fixés par AdaBoost.
Les résultats pour 100 et 1000 étapes de boosting permettent les observations suivantes :
- AdaBoostMG reste le meilleur pour fixer les poids des hypothèses qu'il produit, en particulier lorsque le nombre d'étapes de boosting augmente ;
- a contrario, notre imitation adalike a un meilleur comportement pour un nombre d'étapes de boosting de 100 : ce poids obtient les taux d'erreur les plus faibles sur 10 des vingt problèmes considérés et est le meilleur de tous les poids dans le confrontations deux à deux mais les performances de adalike se dégradent avec l'augmentation du nombre d'étapes de boosting au point de devenir le moins bon de tous les poids étudiés ;
- les poids covering, frequency et même uniform présentent également des résultats intéressants et qui en plus résistent au passage à 1000 étapes de boosting ; covering en particulier semble très proche du poids d'AdaBoost pour 1000 étapes de boosting et tous maintiennent de meilleures performances que celles des systèmes C4.5 et GloBo déjà évalués.
Évaluation expérimentale de GloBoost
Nous évaluons l'algorithme GloBoost muni des différents poids dont nous disposons (adalike, covering, frequency et uniform) :
- à nouveau, notre poids adalike fait apparaître des valeurs aberrantes et supporte mal l'augmentation du nombre d'étapes de boosting.
- les poids covering, frequency et uniform confirment leurs bons résultats au point de concurrencer AdaBoostMG. De plus, cette tendance se confirme lorsque l'on augmente le nombre d'étapes de 100 à 1000 ; même le poids uniform obtient des résultats très honorables en regard de sa simplicité :
- finalement, c'est le poids frequency qui apparaît comme le meilleur de tous : que ce soit à 100 ou à 1000 étapes de boosting, ce poids gagne toutes ces confrontations et obtient le taux d'erreur moyen le plus faible.
Ce résultat est surprenant : ces poids faisaient baisser les performances de AdaBoostMG lorsque celui-ci était utilisé comme générateur et on s'attendait à ce que les taux d'erreur augmentent un peu plus avec un générateur purement aléatoire. Au contraire, ces poids se révèlent mieux adaptés à ce mode de production des hypothèses.
Bilan
Nous avions montré que les résultats sur le boosting laissaient une large place à l'investigation, en particulier sur les apprenants faibles qui peuvent être utilisés. Nous avons étudié ici l'utilisation dans ce rôle de la production de moindres généralisés corrects. Devant la complexité de ce calcul et l'usage intensif que doit en faire AdaBoost, nous avons proposé une génération des hypothèses parallélisable et avons démontré que des poids simples pouvaient ensuite être affectés aux hypothèses. Toutes ces idées ont été validées expérimentalement.
Lectures
Unifying Instance-Based and Rule-Based Induction
Machine Learning Journal 24 (2), 141-168, 1996.
[ version pdf ]
GloBo : un algorithme stochastique pour l'apprentissage supervisé et non-supervisé
In M. Sebag, editor, Actes de la Première Conférence d'Apprentissage, pages 161-168, 1999.
[ version pdf ]
GloBoost : Combinaisons de Moindres Généralisés
Soumis à RIA (octobre 2004).
[ version pdf ]
