Exercice 1 : valeurs et types, expressions et variables

Utiliser la console Python, pour :

1. taper des nombres, des chaînes de caractères, des booléens,
2. taper des opérations arithmétiques, concaténations de chaînes et expressions booléennes,
3. afficher les types des expressions précédentes à l'aide de l'instruction type(),
4. convertir les valeurs obtenues d'un type à l'autre avec les opérateurs str(), bool(), int() et float().

Reprendre ces questions en stockant valeurs et résultats des expressions dans des variables.

Recommencer une dernière fois l'exercice en travaillant, non plus dans la console, mais dans un éditeur de texte et en produisant les affichages avec l'instruction print.

Exercice 2 : l'instruction print

1. Tester l'instruction d'affichage print de Python en affichant successivement un booléen, un nombre, une chaîne de caractères, une variable.
2. Afficher trois valeurs avec une seule instruction print(). Faire apparaître un symbole de votre choix entre les différentes valeurs.
3. Réaliser le même affichage mais sans passer à la ligne à la fin.
4. Effectuer un passage à la ligne sans autre affichage.
5. Utiliser l'instruction help() pour obtenir la documentation de print.

Exercice 3 : tuples en Python

1. Définir dans une variable un tuple décrivant un restaurant à travers quatre éléments : nom, adresse, prix moyen et végétariens bienvenus ou non.
2. Confirmer le type de cette variable à l'aide de l'instruction type().
3. Déballer ce tuple dans quatre variables distinctes et les afficher.
4. Extraire directement le troisième élément du tuple et l'afficher.

Exercice 1 : si alors sinon

1. Définir une variable « température ».
2. Afficher un message différent selon que la température est supérieure à 25° (« allons à la plage ») ou non (« restons à la maison »).
3. En utilisant elif, afficher un message différent (« faut voir ») dans le cas où la température est comprise entre 20 et 25°.
4. En plus de la variable « température », ajouter une variable booléenne indiquant si le ciel est dégagé ou non.
5. Raffiner, selon ce booléen, le cas où la température est entre 20 et 25° : afficher, dans chacun des cas possibles, l'un des deux messages initiaux (plage ou maison).
6. Utiliser des opérateurs booléens pour obtenir le même comportement avec un seul if ... else ....

Exercice 2 : boucle tant que et boucle pour

1. Écrire une boucle while qui affiche les entiers de 1 à 10.
2. Définir un intervalle à l'aide de l'instruction range et des paramètres (1,11). Stocker cet intervalle dans une variable et observer son type.
3. Utiliser une boucle for pour afficher les entiers de cet intervalle.
4. À l'aide de boucles for imbriquées, dessiner des figures géométriques : carrés et triangles, creux ou non.

Exercice 1 : procédures et fonctions

1. Reprendre les instructions produisant des comptages et des figures et les placer dans des procédures avec paramètres.
2. Dans une procédure affichant une figure, rendre le paramètre « symbole » optionnel avec une valeur par défaut. Tester avec un appel ne précisant pas le paramètre optionnel.
3. Réaliser un appel à la procédure en utilisant les noms des paramètres et en changeant l'ordre naturel des paramètres.
4. Implémenter des fonctions Python qui renvoient des figures sous forme de chaînes de caractères, sans affichage.
5. Documenter au moins l'une de ces fonctions à l'aide d'une docstring (voir le cours si nécessaire). Vérifier avec help() l'affichage de cette documentation.

Exercice 2 : modules Python

1. Compléter avec des tests la documentation des fonctions précédentes. À l'aide du module doctest, lancer ces tests.
2. En utilisant la fonction getsizeof() du module sys, observer les tailles en octets des objets déjà créés : entier, réel, caractère, chaîne de caractères, intervalle, tuple, etc.
3. Écrire un module personnel en y plaçant au moins l'une des fonctions ou procédures écrites précédemment. Dans un autre script Python, importer ce module et appeler les procédures rendues ainsi disponibles.

Exercice 1 : lecture et écriture de fichiers

0. Choisir un fichier texte contenant par exemple une œuvre littéraire (à défaut, considérer le fichier horla.txt fourni), dans lequel les paragraphes sont matérialisés par des lignes blanches.
1. En Python, ouvrir le fichier et le parcourir ligne par ligne, afficher chaque ligne.
2. Remplacer les lignes blanches du fichier d'origine par des balises html <BR>.
3. Depuis la console Linux, rediriger les lignes produites par le script Python vers un fichier html.
4. Supprimer cette redirection et programmer en Python la création du fichier html.
5. Travailler (dans le script Python) le document html produit : squelette html5, association à une CSS, utilisation de balises P en lieu et place de BR, repérage d'entités, etc.

Exercice 1 : prise en main des chaînes de caractères

Nous considérons le texte suivant :

Bonjour {prénom} ça va aujourd\'hui ?

1. Définir une variable prénom.
2. Définir neuf variables contenant le texte ci-dessus,
   • en l'encadrant entre apostrophes, entre guillemets ou entre triple guillemets (dans ce dernier cas, on passera une ligne dans le texte d'origine),
   • en utilisant les différentes chaînes de caractères Python (standard, brute ou formatée).
3. Observer le contenu de ces variables dans la console Python.
4. Observer l'affichage produit par l'instruction print pour chacune de ces variables.

Exercice 2 : premières manipulations de chaînes de caractères

Placer dans une variable Python le texte suivant : « Bqrmajv,ok j!w nVqojuéso ,asv egzt ddrédclo daéf ulie, rmdewsmshajgrel.f éPùahsesxedzm yàl vlwaa vqlu e,sdtiinoànz ossuqiévka nfteeé.o ».

Longueur d'une chaîne et accès aux caractères :

1. Afficher la longueur de cette chaîne.
2. Afficher le 13^e caractère.

Extraction de sous-chaînes :

3. Extraire un caractère sur deux et placer le résultat dans une nouvelle variable.

Les questions suivantes, jusqu'à la fin de l'exercice, opèrent sur cette dernière variable.

4. Extraire les sept premiers caractères.
5. Extraire les neuf derniers caractères.
6. Extraire sept caractères à partir du 29^e.

Test d'appartenance et parcours de chaînes :

7. Afficher un message indiquant si la chaîne contient ou non le mot « question ». Idem ensuite avec le mot « Question ».
8. Parcourir la chaîne de caractères avec une boucle et afficher chaque caractère sur une ligne différente.
9. Parcourir la chaîne de caractères pour compter et afficher le nombre d'occurrences de la lettre « e ».

Méthodes des chaînes de caractères :

10. Observer les affichages produits après application des méthodes upper, lower, title, et capitalize.
11. Remplacer le caractère espace par le caractère 😀.
12. Trouver la position de la première occurrence de la lettre « e ». Idem pour la lettre « b ».

Exercice 1 : modifications et parcours de listes

Créations de listes et placement dans des variables :

1. Créer une liste vide, puis une liste contenant des éléments.
2. Créer des listes à partir d'objets existants : depuis un intervalle, depuis une chaîne de caractères, depuis une autre liste.
3. Construite une liste de mots à partir d'une phrase placée dans une chaîne de caractères. Reconstituer une chaîne de caractères à partir de la liste, sans séparateur entre les mots cette fois.

Choisir l'une des listes précédemment créées pour la suite de l'exercice.

4. Afficher la liste et sa longueur.
5. Remplacer l'une des valeurs par une nouvelle valeur.
6. Supprimer la deuxième case.
7. Supprimer une autre case en ciblant la valeur contenue dans la case.
8. Ajouter deux nouvelles valeurs : l'une en fin de liste, l'autre en troisième position.
9. Afficher à nouveau la liste et sa longueur.
10. Utiliser une boucle pour parcourir les éléments de la liste et les afficher un par un. Passer en revue les différentes syntaxes possibles pour cette boucle.

Exercice 2 : tableaux de nombres

0. Définir en Python un tableau d'entiers.

Écrire (et valider sur le tableau déjà défini) les fonctions qui :

1. calcule la moyenne des nombres contenus dans un tableau donné,
2. compte le nombre d'occurrences d'un élément,
3. compte combien d'éléments sont supérieurs ou égaux à 10,
4. recherche la valeur maximale du tableau,
5. teste si un élément est présent ou non (envisager plusieurs algorithmes et différentes syntaxes Python).

Exercice 1 : implémentation d'un type produit

1. Implémenter en Python, à l'aide de dictionnaires) le type abstrait « Étudiant » (composé d'un nom, d'un prénom, d'une année de naissance, d'une note en informatique et d'une note en littérature).
2. Bien travailler en particulier la procédure dont le rôle est d'afficher un étudiant.
3. Créer quelques étudiants et tester chacune des fonctions.

Exercice 2 : tableaux d'enregistrements, les étudiants

1. Créer une promotion comme un tableau d'étudiants,
2. implémenter la fonction moyenne d'un étudiant dédiée cette représentation,
3. pour chaque discipline, la fonction moyenne de la promotion,
4. la fonction qui trouve l'étudiant ayant eu la note moyenne maximale.
5. Généraliser à un type d'étudiant qui possède un nombre quelconque de notes.

Exercice 1 : recherche de mots particuliers

Pour chaque motif ci-dessous, implémenter en Python le parcours du fichier-dictionnaire et afficher les mots qui respectent la contrainte.

1. Débute par une voyelle.
2. N'est composé que de voyelles.
3. Ne contient aucune voyelle (ni en majuscule, ni en minuscule).
4. Comporte au moins deux x.
5. Comporte exactement deux x.
6. Comporte trois y.
7. Comporte quatre z.
8. Contient au moins un caractère qui n'est pas une lettre.
9. N'est composé que de lettres majuscules.
10. Est un palindrome.

Exercice 2 : édition d'un catalogue de jouets

Un catalogue de Noël nous est fourni sous forme d'un fichier CSV et d'un dossier contenant des photos des jouets.

1. Programmer en Python le parcours du fichier.
2. Sur chaque ligne, récupérer le code du jouet, son intitulé et sa description.
3. Mettre en page ces informations dans un document html/css produit automatiquement.
4. Faire apparaître l'image associée à chaque jouet (si elle est disponible).
5. Répérer et distinguer négativement les jouets utilisant des piles.
6. Mettre en avant l'âge éventuellement associé à chaque jouet.

Envisager des variations sur le script écrit pour produire, non plus de l'html, mais d'autres formats textuels : Markdown, LaTeX, XML/TEI, etc. Utiliser ensuite les outils adéquats pour créer des documents pdf, epub, etc.

Exercice générique

1. Écrire un parser SAX qui affiche tous les événements déclenchés (début et fin de document, début et fin d'élément, feuilles textes).
2. Écrire un parser SAX qui compte le nombre de balises ouvrantes dans le document XML.
3. Écrire un parser SAX qui compte le nombre d'occurrences de chaque balise.
4. Écrire un parser SAX qui regroupe les feuilles textes non séparées par des balises.

Squelette XML indenté

Fournir un programme Python basé sur SAX qui présente les balises d'un fichier XML quelconque de manière arborescente, c'est-à-dire :

• un nom d'élément par ligne ;
• une indentation proportionnelle à la profondeur du noeud dans l'arbre.

Le championnat : calcul de statistiques et production XHTML

Écrire un programme Python qui utilise SAX pour lire un fichier de type Foot. Celui-ci devra produire les mêmes sorties que la feuille XSLT écrite précédemment et, en plus, des statistiques par équipe (nombre de matches joués, de victoires, de points, différence de buts, etc.). Étape par étape :

1. sortie HTML des matches ;
2. calcul et affichage de statistiques ;
3. produire un sommaire de la page et le placer en fin de document ;
4. faire apparaître ce sommaire en tête de page.

Acteurs

Écrire un programme Python basé sur l'API SAX qui, qui pour tout fichier XML respectant notre DTD acteurs.dtd, produit une version html présentant :

• le contenu,
• un sommaire,
• les références résolues.

TODO list

Il s'agit d'écrire un programme Python basé sur l'API SAX et produisant une sortie HTML, bien formé et contenant un maximum d'informations de la todolist (idéalement toutes !), par exemple :

• un titre dans l'en-tête et un titre dans le corps qui reprennent le nom du propriétaire de la liste ;
• l'image associée à chaque todo ;
• le titre de chaque todo à l'aide d'un élément HTML adéquat ;
• également sa date limite ;
• ensuite, les paragraphes des commentaires ;
• puis, les items rassemblés sous la forme d'une liste HTML, les items critiques étant distingués des autres ;
• les liens (qui doivent être cliquables), les dates et les mots importants contenus dans les parties textuelles.

Extraction de méta-données

Écrire un script Python utilisant l'API DOM qui, à partir d'un fichier SVG (comme tux ou argentina), fournit les informations suivante :

• le nom de l'auteur du dessin ;
• le titre du dessin ;
• la liste des mots clés qui lui est associée ;
• le nombre de rectangle utilisés (élément rect) ;
• la taille de ces rectangles (attributs height et width).

Exemple de sortie attendue :

-- le nom de l'auteur --
L'auteur est Rory McCann !
-- le titre du dessin --
Baby Tux
-- les mots clefs --
baby
linux
bird
penguin
mascot
tux
animal
computer
cute
-- les rectangles --
il y en a 4 :
  .  42.034428  x  39.407280
  .  42.034428  x  39.407280
  .  61.150040  x  211.13000
  .  57.995739  x  207.72755

Fonctions utiles

À la suite de l'exercice précédent, il semble opportun de disposer des fonctions Python suivantes :

• getAttributeValue(n,a) : fournit la valeur de l'attribut nommé a et associé au noeud élément n ;
• getChildElementsByTagName(n,tag) : fournit la liste des éléments fils du noeud n et nommés tag ;
• getTextContent(n) : fournit le contenu textuel associé au noeud élément n ;
• resolveElementsPath(dom,path) : path étant une liste de noms d'éléments (e₁,e₂,...e_n), cette fonction fournit les noeuds vérifiant la requête XPath //e₁/e₂/.../_n dans la représentation dom.

Programmer ces fonctions en s'appuyant sur l'API DOM de Python. Reprendre l'exercice précédent en utilisant les fonctions nouvellement créées.

Le championnat : calcul de statistiques et production XHTML

Écrire un programme Python qui utilise DOM pour lire un fichier de type Foot et produire :

1. calcul de statistiques sur le championnat (nombre de journées, de matches, taux de victoires à domicile, etc.) ;
2. produire une version XHTML des matches et des résultats ;
3. produire pour cette page un sommaire apparaissant en tête de document.

Caractéristiques de l'arbre DOM

1. Écrire un parser qui compte le nombre de balises ouvrantes dans un document XML quelconque ;
2. écrire un parser qui compte le nombre d'occurrences de chaque balise ;
3. proposer et tester une fonction qui renvoie la liste des noeuds feuilles d'un arbre DOM ;
4. proposer et tester une fonction qui calcule la hauteur d'un arbre DOM.

Caractéristiques d'un noeud

Écrire et tester les fonctions qui réalisent les tâches suivantes :

1. déterminer si un noeud est la racine de l'arbre DOM ou pas ;
2. renvoyer la liste des ancêtres d'un noeud (du noeud vers la racine, puis vice-versa) ;
3. renvoyer la liste des noeud frères gauches d'un noeud donné.

Parcours d'arbres

Afficher les noeuds d'un document XML suivant les différents parcours possibles d'un arbre. En particulier, vous testerez votre programme sur un document XML représentant une expression arithmétique, comme par exemple :

<expression op="+">
  <value x="5" />
  <expression op="*">
    <value x="7" />
    <value x="6" />
  </expression>
</expression>

Compter des noeuds

Écrire en Python et à l'aide de DOM une fonction qui compte dans un document XML quelconque le nombre de fois où un attribut donné apparaît avec une valeur particulière. Un appel à cette fonction pourrait ressembler à :

xmlfilename = sys.argv[1]
dom         = parse(xmlfilename)

n = CountAttributeValue(dom,'lang','fr')

print n

Modifier l'arbre DOM

Reprendre le document Foot :

• le charger dans une structure DOM ;
• créer une structure DOM vide ;
• y placer toutes les informations du fichier d'origine mais organisées par équipe et non plus par journée ;
• produire un nouveau fichier XML à partir de ce DOM.

Tortue

(voir détails dans le cours Python)

1. Utiliser la tortue pour dessiner un carré plein, puis une ligne de carrés et enfin un carré de carrés.

Exercice 1 : noms d'agents

Nous souhaitons, dans cet exercice, programmer le processus qui transforme un verbe en nom d'agent (par exemple chanter donne chanteur).

Application à un unique verbe :

1. Définir une variable Python contenant un verbe du premier groupe.
2. Extraire son radical.
3. Ajouter le suffixe -eur au radical et afficher le résultat.

Généralisation à plusieurs verbes :

4. Écrire une procédure qui reprend les instructions précédemment écrites.
5. Tester cette procédure sur quelques verbes bien choisis.
6. Placer des verbes du premier groupe dans une liste Python.
7. Parcourir cette liste et appeler la procédure sur chaque verbe.

Utilisation de fichiers :

8. Créer un fichier texte contenant quelques verbes, un par ligne.
9. Lire ce fichier de verbes depuis le script Python.
10. Appliquer la procédure à chaque verbe du fichier.
11. Produire les résultats dans un fichier html.

Extension à un fichier dictionnaire :

12. Lire un fichier dictionnaire contenant tous les mots de la langue française.
13. Appliquer la procédure à chaque mot se terminant par -er.
14. Placer le résultat dans le fichier html, si et seulement si nom obtenu est dans le dictionnaire.

Exercice 2 : conjugaison automatique

1. Définir une liste de pronoms et des listes de terminaisons (pour les premier et deuxième groupes au présent de l'indicatif).
2. Définir une variable contenant un verbe.
3. Extraire le radical du verbe.
4. Programmer une boucle qui parcourt et affiche les pronoms.
5. À chaque pronom, ajouter le radical du verbe.
6. Compléter chaque ligne produite par la terminaison adéquate.
7. Généraliser en procédure, stocker des verbes dans une liste, parcourir la liste et appeler la procédure sur chaque verbe.
8. Lire les verbes depuis un fichier textuel.
9. Produire un document html/css présentant les verbes conjugués.
10. Adapter la méthode aux cas particuliers : aimer, manger, commencer, devancer, etc.

Exercice 3 : préfixations en dé-

Nous nous intéressons cette fois à l'inversion du sens d'un verbe par préfixation en dé-. Par exemple, le verbe mêler donne le verbe inverse démêler. Nous serons vigilants à ce que notre procédure fonctionne en particulier sur les verbes suivants : chanter, mêler, axer, boucher, saler, équilibrer, hydrater et stabiliser.

1. Écrire sur papier l'algorithme qui traite correctement l'ensemble des verbes cités.
2. Programmer cet algorithme en Python et tester sur un verbe.
3. Généraliser le traitement en procédure.
4. Placer les verbes dans une liste Python et appeler la procédure sur chaque verbe.
5. Utiliser deux fichiers : l'un pour y lire les verbes à traiter, l'autre pour recevoir les résultats au format html.

Exercice 1 : tableaux d'enregistrements, les restaurants

Préliminaires

0. Récupérer le dossier tp-restos.
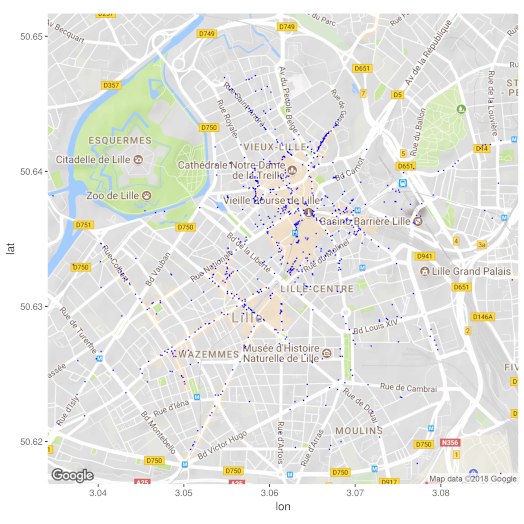
   Une liste de restaurants vous est fournie et, pour chaque restaurant, vous pouvez accéder à son nom, son adresse (à travers num et rue), sa localisation exprimée cette fois en latitude et longitude (lat et lon), sa position dans le classement (pos), sa note et le nombre d'avis qui ont été émis sur ce restaurant (votes).
   Ci-dessous les premières lignes du fichier exercices.py qui montrent la récupération des restaurants, l'accès au classement et au nom d'un restaurant, et enfin une boucle sur la liste des restaurants.

from restos import liste_restos

# affichage des informations sur un restaurant
# à compléter
def affiche_resto (resto):
    print('[',resto.get('pos'),']',end=' ')
    print(resto.get('nom'))
    print()

# boucle sur tous les restaurants, pour affichage
for resto in liste_restos:
    affiche_resto(resto)

1. Compléter l'affichage d'un restaurant. Appliquer à tous les restaurants de la liste.

Notes et avis

2. Afficher le nombre de restaurants disponibles.
3. Calculer combien d'avis ont été donnés au total. Combien d'avis a reçus un restaurant en moyenne ?
4. Afficher la moyenne des notes, ainsi que l'écart-type.
5. Afficher le nombre de restaurants ayant une note de 4,5 ou plus.

Localisation/identification des restaurants

6. Calculer la moyenne des latitudes et des longitudes. À quel endroit correspondent ces coordonnées (utiliser par exemple ce site ou directement Google Maps pour visualiser sur une carte la localisation calculée) ?
   Idem avec uniquement les restaurants ayant reçu plus de 50 avis.
7. Indiquer si oui ou non il y a un restaurant dans la rue alphonse mercier. Idem avec la rue du port.
8. Afficher la description du restaurant classé à la première position. Idem avec le restaurant placé à la dernière position.
9. Afficher toutes les informations disponibles sur le restaurant la ducasse. Idem pour le restaurant qui se trouve au 14 rue des postes.
10. Produire la liste des restaurants se trouvant rue du molinel.
11. Identifier le restaurant ayant reçu le plus d'avis.

Coup d'œil en arrière

La liste_restos jusque là utilisée correspond à la dernière année disponible. Le code Python ci-dessous vous permet d'accéder aux informations sur les restaurants pour les années précédentes.

# récupération des archives
from restos import archives

# constitution de la liste des restaurants 2018
liste_restos_2018 = archives["2018"]

12. Reprendre les mêmes questions pour l'année précédente. Si ce n'est déjà fait, c'est le bon moment pour utiliser procédures et fonctions.
13. Quels sont les restaurants qui sont apparus lors de la dernière année ?
    Des restaurants se trouvaient-ils à la même adresse ?
    Quels restaurants ont disparu ?
14. Identifier le restaurant qui a le plus progressé dans le classement.
    Identifier le restaurant qui a chuté le plus durement.
15. Montrer l'évolution d'un restaurant donné au fil des années.

Adresses et rues

16. Détecter les adresses partagées par plusieurs restaurants.
17. Identifier la ou les rue(s) ayant le plus de restaurants.
18. Trouver la meilleure rue pour les restaurants (la rue avec la meilleure moyenne de notes, ou les rues où chaque restaurant a une note strictement supérieure à 4, etc.).
19. Idem avec la rue à ne pas fréquenter pour ses restaurants.

Il est possible de reprendre les deux dernières questions en jugeant une rue, non plus sur la moyenne des notes de ses restaurants, mais sur leur classement moyen.

Plus encore...

20. Afficher les restaurants par ordre de classement.
21. Reprendre les questions impliquant des calculs de moyennes et calculer cette fois des médianes.
22. Produire une cartographie des restaurants lillois. Par exemple, une telle cartographie des restaurants est jugée satisfaisante.

Exercice 2 : algorithmes avancés sur les tableaux

Sur les tableaux quelconques

1. Implémenter une fonction index_minimum(t,d,f) qui renvoie le numéro de la case contenant la plus petite valeur du tableau t entre les cases d et f.
2. Programmer un tri à bulles.

Sur les tableaux déjà triés

On suppose disposer d'un tableau de nombres rangés par ordre croissant.

1. Implémenter une fonction de recherche d'un élément utilisant une boucle tant que et tirant parti du fait que les éléments sont ordonnés.
2. Écrire une fonction de recherche dichotomique.
3. Proposer une procédure insertion(e,t,n) qui ajoute un élément e à sa place dans un tableau t de taille n.

Autres méthodes de tri

1. tri_extraction utilisant index_minimum(t,d,f) : on récupère le minimum du tableau et on le place dans la première case, on récupère le minimum du tableau privé de la première case et on le place dans la deuxième, etc.
2. tri_insertion utilisant insertion(e,t,n) : prendre le i^ème élément et le mettre à sa place dans les i-1 premières cases déjà triées.

Exercice 3 : Comparaison expérimentale des méthodes de tri

Préliminaires

On veut dans cette séance comparer les méthodes de tri (comme le tri à bulles par exemple) en terme de temps de calcul et en fonction de la taille et de la nature des tableaux à trier.

De nouveaux points techniques sont nécessaires, essentiellement : savoir produire des fichiers texte en Python (voir détails dans le cours Python) et connaître les bases de gnuplot.

gnuplot est un outil qui permet de tracer des courbes à partir de données brutes. Par exemple, l'instruction :

$ gnuplot
gnuplot> plot 'stats.dat' with lines

permet de tracer les points qui se trouvent dans le fichier stats.dat sous la forme suivante (un point par ligne, valeur en abscisse, une tabulation, valeur en ordonnée) :

100     2
200     14
300     26
400     48
500     72
600     111
700     142
800     194
900     238
1000    298

C'est ce type de fichier que l'on veut faire produire par Python (la première colonne pourrait correspondre aux tailles des tableaux considérés, la seconde aux temps de traitement nécessaires).

Fonctions à implémenter

1. Écrire une fonction copie (t) qui renvoie un nouveau tableau contenant dans le même ordre les mêmes valeurs que le tableau t ; vérifier qu'une modification de la copie n'altère pas le tableau original.
2. Proposer une fonction inverse (t) qui fournit un nouveau tableau contenant les mêmes valeurs que le tableau t mais dans l'ordre inverse.
3. Implémenter des fonctions pour produire des tableaux :
   • une fonction tableau_premiers_entiers (n) qui produit un tableau contenant dans l'ordre tous les entiers de 1 à n,
   • une fonction tableau_premiers_entiers_melanges (n) qui propose ces mêmes entiers mélangés aléaoirement,
   • une fonction tableau_premiers_entiers_inverses (n) qui propose ces mêmes entiers du plus grand au plus petit.
4. Proposer une procédure ligne_dans_fichier (f,n,t) dont le rôle est d'écrire dans le fichier f la valeur (numérique) de n, une tabulation, la valeur (numérique) de t et enfin un passage à la ligne.
5. Écrire une fonction temps_tri_bulles (t) qui fait une copie du tableau t et renvoie le temps nécessaire au tri à bulles pour classer cette copie.
6. Coder la procédure stats_melange (nmin,nmax,pas,fois) qui pour chaque taille de tableau comprise entre nmin et nmax en avançant de pas en pas produit fois tableaux mélangés aléatoirement et écrit dans un fichier le temps moyen nécessaire au tri à bulles pour classer ces tableaux.
7. Même question avec la fonction stats_ordonne (nmin,nmax,pas,fois) pour des tableaux déjà ordonnés.
8. Même question avec la fonction stats_inverse (nmin,nmax,pas,fois) pour des tableaux déjà ordonnés mais en ordre inverse.
9. Produire à l'aide de votre code des fichiers de statistiques pour des tailles de tableau variant de 100 en 100, entre 100 et 1000, avec 5 répétitions pour chaque taille de tableau. Visualiser ces données avec gnuplot et comparer l'évolution du temps nécessaire au tri bulles selon le type de tableaux et selon leurs tailles.
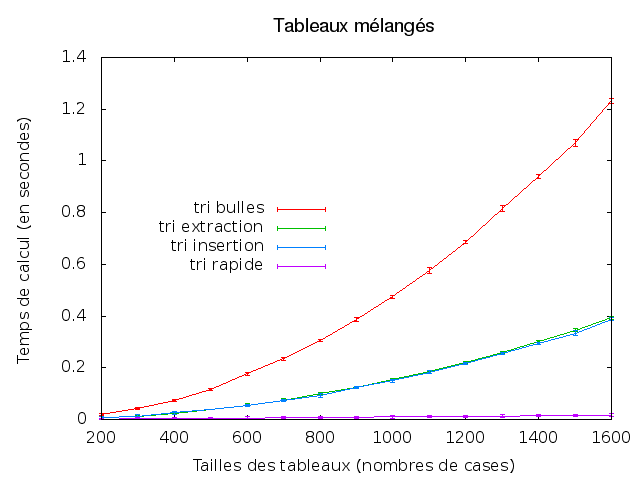
10. Généraliser votre code pour pouvoir également comparer les méthodes de tri entre elles : tri à bulles, tri insertion, tri extraction et tri rapide.
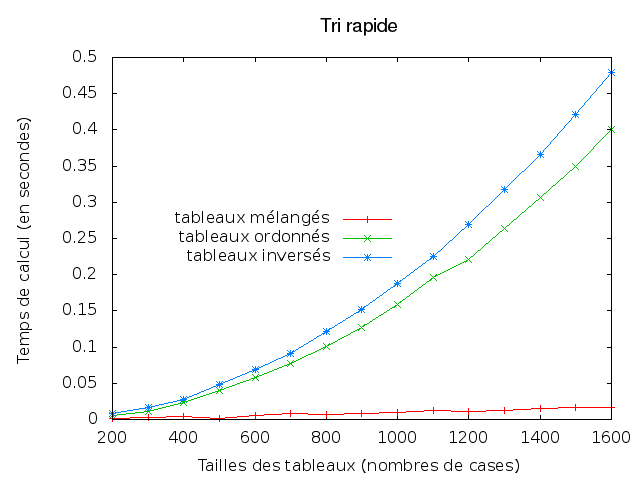
11. Tester des modifications des méthodes de tri, calculer les écarts-types des temps de calcul sur les tableaux mélangés, explorer les possibilités de gnuplot, expliquer théoriquement les courbes obtenues.

Au final, on doit obtenir des images comme celles-ci :

Exercice 4 : Conjecture de Syracuse

Explications

Ce problème est apparu pour la première fois dans les années 30. Puis, à nouveau, à l'université de Syracuse (New York) dans les années 50. Aucune solution n'étant trouvée, le problème s'est propagé aux autres universités américaines. Dans le contexte de la guerre froide, on évoque (comme une plaisanterie ?) une manœuvre russe pour paralyser la recherche américaine.

L'énoncé de ce problème est le suivant. On part d'un entier n auquel on fait subir une transformation :

• si n est pair, on le divise par deux ;
• si n est impair, on le multiplie par 3, et ajoute 1.

Puis, on recommence sur le résultat. Par exemple, en partant de n=10, on obtient :

Conjecture : quel que soit l'entier n, on finit par retomber sur 1.

Implémentations Python

1. Définir la carte d'identité d'un entier comme l'enregistrement de :
   • cet entier,
   • sa trajectoire (les entiers rencontrés jusqu'à 1),
   • sa durée de vol (le nombre d'entiers rencontrés avant de trouver 1),
   • son altitude maximale (le plus grand entier rencontré).
2. Proposer une procédure qui affiche une telle carte.
3. Écrire une fonction qui permet de tester la conjecture pour un entier donné et qui renvoie sa carte d'identité renseignée.
4. Écrire ensuite une fonction qui teste tous les entiers dans un intervalle donné et renvoie toutes les cartes d'identité de ces entiers.
5. Utiliser cette fonction pour afficher les cartes présentant une durée de vol strictement supérieure à 100.
6. Implémenter un tri à bulles pour classer des cartes par altitude décroissante.

Exercice 5 : Chiffrement et décryptage

Préliminaires

Dans cette séance, on s'intéresse au chiffrement de textes par substitution, à leur déchiffrement, et enfin au moyen de casser un tel cryptage. Un chiffrement par substitution consiste simplement à remplacer systématiquement une lettre par une autre.

Certains chiffrements par substitution sont dits par décalage ou appelés chiffre de César : dans ces cas, une lettre et sa remplaçante sont toujours séparées dans l'alphabet par le même nombre de lettres. Un chiffrement par décalage répandu sur le web se nomme ROT13 : une lettre et sa remplaçante sont à une distance de 13 dans l'alphabet (le a est remplacé par le n, le b par le o, etc.).

Par souci de simplicité, on ne considère que des textes en minuscules, sans accent et sans symbole de ponctuation. Seul l'espace est utilisé entre les mots mais n'est pas remplacé par le chiffrement.

Cette séance va nécessiter de traiter des chaînes de caractères qu'il peut être commode de voir comme des listes de caractères, ce que permet Python.

Concernant les caractères eux-mêmes, on rappelle qu'il est possible de repérer un caractère par un numéro (son code ASCII).

Nous aurons également besoin de stocker les correspondances entre lettres, ce qui peut être fait à l'aide de dictionnaires Python (que nous avions déjà utilisés pour coder des enregistrements).

Enfin, pour décrypter un texte sans connaître la règle de chiffrement, il est courant d'utiliser la fréquence d'apparition des lettres dans la langue choisie. On considérera qu'en français les lettres se rangent comme suit, de la plus fréquente à la moins fréquente :

e a i t s n l u r o d m c p v q h f b g j x y w z k

Fonctions à implémenter

On va d'abord réaliser et tester quelques fonctions pour gérer les dictionnaires, chiffrer et déchiffrer des textes.

1. chiffrement_lettre (l,d) renvoie la correspondance de la lettre l dans le dictionnaire d si cette correspondance existe, renvoie la lettre l elle-même sinon.
2. chiffrement_phrase (p,d) construit une nouvelle chaîne de caractères correspondant au chiffrement caractère par caractère de la phrase p à l'aide du dictionnaire d. Définir un dictionnaire et tester ces fonctions en codant une phrase quelconque.
3. inverse_dico (d) renvoie un nouveau dictionnaire qui inverse les clefs et les valeurs du dictionnaire d. Tester en déchiffrant la phrase précédemment codée.
4. dico_rot_13 () construit un dictionnaire correspondant au chiffrement en ROT13. Tester à nouveau pour chiffrer une phrase quelconque. Quelles solutions sont possibles pour le déchiffrement ?

On veut maintenant déchiffer un texte codé par une technique de substitution mais on ne dispose pas du dictionnaire utilisé. L'objectif est de décoder le texte mystère suivant.

Les étapes à réaliser sont les suivantes.

5. compte_lettres (p) construit un dictionnaire faisant correspondre chaque lettre apparaissant dans la phrase p à son nombre d'occurrences dans cette même phrase. Tester sur le texte mystère.
6. tri_bulles_dico (d) est un tri à bulles modifié pour renvoyer les clefs d'un dictionnaire d, ordonnées par valeurs décroissantes. Tester sur le dictionnaire précédemment calculé par compte_lettres.
7. arrays2dict (ks,vs) renvoie un dictionnaire dont les clefs correspondent au tableau ks et qui associe pour chacune de ces clefs la valeur se trouvant à la même position dans le tableau vs. Utiliser cette fonction pour combiner le tableau fourni par tri_bulles_dico et le tableau des lettres de l'alphabet classées par fréquences décroissantes dans la langue française.
8. decrypte (pc,ll) doit décrypter la phrase pc à l'aide des lettres de l'alphabet rangées par ordre de fréquence décroissante dans la langue utilisée et disponible dans le tableau ll. Décoder le texte mystère à l'aide de cette fonction.

Exercice 1 : Implémentation du type abstrait « Entier »

1. Implémenter le type abstrait « Entier » vu en cours en utilisant... les entiers de Python.
2. Coder les opérations addition et multiplication sur ce nouveau type.
   [ voir la correction ][ récupérer ]
3. Implémenter à nouveau le type abstrait « Entier » vu en cours cette fois en s'appuyant sur les listes de Python (une liste de n éléments quelconques représentera l'entier n).
   [ voir la correction ][ récupérer ]
4. Est-il nécessaire de recoder les opérations addition et multiplication ?

Exercice 2 : Implémentation du type abstrait « Pile »

1. Implémenter le type abstrait « Pile » vu en cours.
2. Écrire une fonction qui permet d'inverser une pile.
3. Écrire une fonction qui prend en entrée un texte composé de différentes parenthèses, accolades, crochets, ouvrants ou fermants, et qui vérifie que l'expression est bien parenthésée.
   On pourra par exemple suivre les étapes suivantes :
   • une fonction qui prend en entrée un caractère et renvoie vrai s'il s'agit d'un symbole ouvrant et faux sinon,
   • une fonction qui prend un symbole ouvrant et fournit en retour le caractère fermant correspondant,
   • enfin, la fonction de vérification.
4. Écrire une fonction qui évalue une expression polonaise inversée, composée d'entiers entre 0 et 9 et des quatre opérations élémentaires.
   On pourra par exemple suivre les étapes suivantes :
   • une fonction qui prend en entrée un caractère et renvoie vrai s'il s'agit d'une opération élémentaire et faux sinon,
   • une fonction qui prend un symbole-opération et deux entiers et qui renvoie le résultat de l'opération,
   • enfin, la fonction d'évaluation.