De la nécessité des biais en apprentissage automatique

Saut inductif

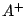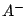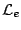Le but de l'apprentissage est de pouvoir décider si un exemple, jamais vu auparavant, appartient au concept étudié ou non. Pour cela, nous avons à notre disposition, les ensembles d'exemples positifs et négatifs , tous décrits à l'aide d'un langage . Leur disjonction constitue ce que l'on appelle un apprentissage par cœur, et ne dit rien sur la classe d'un nouvel exemple : il faut impérativement généraliser les exemples positifs de 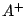, en évitant de couvrir les contre-exemples de .

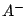Cette généralisation est appelée un saut inductif, mais ce saut est périlleux. Il revient, en quelque sorte, à imaginer l'ensemble du concept en n'observant qu'une partie de ce concept. Le mot imaginer peut paraître déplacé dans un cadre scientifique, pourtant ce choix se justifie puisqu'il reflète toute la difficulté de fonder la généralisation.

Le No Free Lunch Theorem indique même que cette tâche est impossible : quelle que soit la méthode de généralisation, le taux de bonnes prédictions sera en moyenne de 0.5 sur l'ensemble des problèmes possibles. Si bien que toute méthode de généralisation est aussi fondée que le classement aléatoire des nouveaux exemples.

Laissons de côté, pour l'instant, ce résultat négatif pour discuter du rôle des biais dans le saut inductif.

Nécessité des biais

Tom Mitchell définit un biais comme tout moyen de préférer une généralisation à une autre, chacune d'elles étant correcte et complète vis-à-vis de 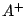et 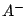. En d'autres mots, un biais nous permet de choisir entre deux généralisations qui sont équivalentes pour le problème d'apprentissage.

D'après Tom Mitchell, les biais peuvent opérer à deux niveaux :

• sur le langage des hypothèses, en fixant la forme que devra avoir la solution ;
• sur la procédure de recherche d'une généralisation satisfaisante dans le langage des hypothèses, en indiquant comment cette recherche doit opérer.

Pour se convaincre de l'intérêt des biais et plus encore, de leur absolue nécessité, reprenons la démonstration qu'en a donnée Tom Mitchell, en construisant un système non biaisé, c'est-à-dire dont les deux niveaux évoqués ci-dessus sont exempts de biais.

• Tout d'abord, il nous faut un langage 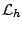permettant de représenter les hypothèses qui soit absolument sans biais : pour cela, ce langage doit permettre de caractériser n'importe quelle partition du langage des exemples 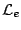en deux sous-ensembles, 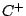et 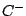. Dans la terminologie de Vapnik, nous voulons que 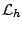pulvérise 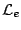. De plus, nous voulons définir un tel 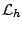sans pour autant poser quoi que ce soit sur la forme des hypothèses. Pour cela, nous choisissons de voir une hypothèse comme l'ensemble 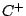des exemples qu'elle couvre ; ainsi, chaque sous-ensemble du langage des exemples 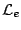est une hypothèse.
• L'étape suivante consiste à trouver une procédure de recherche sans biais, c'est-à-dire qui ne favorise aucune généralisation en particulier. Il nous faut donc construire l'ensemble de toutes les généralisations des exemples positifs qui ne couvrent pas de négatifs, ensemble que Tom Mitchell nomme espace des versions.

  Dans notre langage des hypothèses, une hypothèse appartient à l'espace des versions si et seulement si elle inclut tous les exemples posi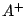tifs de , et aucun des exemples négatifs de 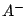. Les hypothèses de l'espace des versions se distinguent les unes des autres par les exemples étrangers à l'ensemble d'apprentissage qu'elles contiennent ou non. L'espace des versions est donc défini par :

  

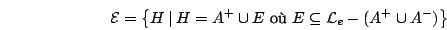
Voyons maintenant comment il est possible de classifier de nouveaux exemples à partir de cet espace des versions, en prenant toujours garde à ne pas introduire de biais.

• Comme nous nous refusons à choisir une des généralisations candidates, nous ne pouvons garantir qu'un exemple est positif que s'il est couvert par toutes les généralisations de l'espace des versions. Or, si un exemple apparaît dans chacune des hypothèses de l'espace des versions, cela ne peut signifier qu'une chose : l'exemple est un exemple positif de l'ensemble d'apprentissage ; en effet :
  
• De même, un exemple sera étiqueté négatif s'il n'est couvert par aucune des généralisations de l'espace des versions. À nouveau, cela n'est possible que si l'exemple était connu comme négatif au moment de l'apprentissage car :
  
• Dans les autres cas, les généralisations de l'espace des versions ne sont pas unanimes et nous ne pouvons pas trancher sans introduire de biais : l'exemple reste de classe inconnue.

Ceci montre, très simplement, qu'un apprentissage sans biais ne permet de classifier que les exemples dont la classe est déjà connue. Autrement dit, sans autre information que les exemples étiquetés, il ne peut pas y avoir de saut inductif et donc pas d'apprentissage.

Finalement, il n'y a pas d'autre choix que de biaiser l'apprentissage, et ce que nous avons nommé imagination passe par ces biais.

Justification des biais

Maintenant qu'il est établi que les biais doivent être utilisés, reste à déterminer quels sont les biais disponibles et, parmi ces derniers, identifier ceux qui ont un sens pour le problème considéré. Tom Mitchell identifie plusieurs biais justifiables :

• Tout d'abord, il y a les connaissances liées à un problème, à un domaine particulier, et rassemblées sous le nom théorie du domaine. Par exemple, dans un problème lié à la caractérisation de liens familiaux, le fait qu'un individu ne peut pas être à la fois père et mère pourra être utilisé.
• Ensuite, la manière dont le résultat sera utilisé est parfois une information pertinente. Dans le cas de molécules cancérigènes, il est préférable d'indiquer à tort qu'une molécule est cancérigène et de ne pas l'utiliser, plutôt que de cataloguer comme non cancérigène une molécule cancérigène et ainsi autoriser la diffusion d'un produit dangereux. Pour le concept est_cancérigène, les définitions les plus générales possibles de ces molécules seront favorisées.
• La connaissance de la source des exemples peut être utilisée en cours d'apprentissage : l'apprenti peut essayer de deviner ce que l'on veut lui faire apprendre, connaissant l'enseignant.
• Il est courant de privilégier la simplicité de la solution. La validité de ce biais est une simple application du rasoir d'Occam. Sa mise en œuvre est souvent plus délicate mais cela dépasse le cadre de cette discussion.
• Enfin, l'analogie avec des cas déjà traités peut amener des biais intéressants, par exemple en découvrant une caractérisation des généralisations les plus pertinentes pour un certain type de problème.

Lectures