Cadre PAC (Probably Approximately Correct)
Origine
Le modèle PAC a défini par Leslie G. Valiant en 1984. L'une des motivations est de caractériser formellement les langages qui sont apprenables automatiquement à partir d'exemples, ceux qui ne le sont pas et également lequel de deux langages est plus facilement apprenable que l'autre.
On retrouve en fait dans la définition du modèle PAC une volonté de classifier les problèmes d'apprentissage comme on classe les problèmes en calculabilité et complexité.
Notations et protocole
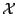 : l'espace de description des exemples ;
: l'espace de description des exemples ;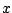 : un exemple particulier ;
: un exemple particulier ; 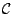 : une classe de concepts définis sur
: une classe de concepts définis sur
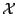 ;
;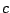 : un concept particulier ; on peut avoir deux vues d'un même concept :
: un concept particulier ; on peut avoir deux vues d'un même concept :
- une vue purement ensembliste où
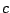 est l'ensemble des exemples appartenant au concept
(
est l'ensemble des exemples appartenant au concept
(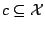 ) ;
) ;
- une vue fonctionnelle où
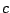 est une fonction booléenne sur les exemples
est une fonction booléenne sur les exemples
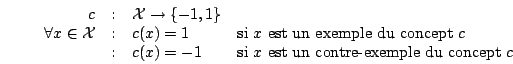
- une vue purement ensembliste où
 une distribution sur
une distribution sur
 ;
;- l'erreur d'une hypothèse
 par rapport à un concept cible
par rapport à un concept cible
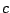 est définie comme la
probabilité de trouver un exemple sur lequel
est définie comme la
probabilité de trouver un exemple sur lequel
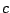 et
et 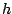 sont en désaccord :
sont en désaccord :
![\mbox{erreur}(h) = \mbox{Pr}_{x \in \cal D} \left[ c(x) \neq h(x) \right]](/Enseignement/Cours/Apprentissage-Automatique/pac/img9.png)
- enfin, on suppose l'existence d'un orable noté
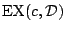 ; à chaque appel, cet
oracle tire un exemple de
; à chaque appel, cet
oracle tire un exemple de 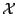 suivant
suivant 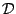 et fournit cet exemple avec sa classe
et fournit cet exemple avec sa classe
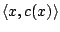 .
.
Dans ce cadre, l'objectif est d'apprendre rapidement une hypothèse
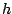 de faible erreur, avec peu
d'appels à l'oracle.
de faible erreur, avec peu
d'appels à l'oracle.
Une instanciation possible :

Notion d'apprenabilité (forte)
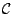 est PAC-apprenable s'il existe un algorithme
est PAC-apprenable s'il existe un algorithme
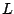 tel que
tel que
- pour tout concept
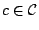 ,
,
- pour toute distribution
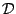 sur
sur
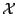 ,
,
- pour tout
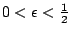 ,
,
- pour tout
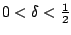 ,
,
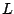 fournit une hypothèse
fournit une hypothèse
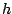 de
de
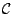 qui, avec une probabilité
qui, avec une probabilité
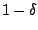 , vérifie :
, vérifie :

Remarques sur la définition d'apprenabilité :
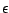 est appelé paramètre d'erreur,
est appelé paramètre d'erreur,
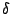 paramètre de confiance ;
paramètre de confiance ;
- on veut pouvoir rendre
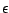 et
et 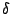 arbitrairement petits, à faible coût ;
arbitrairement petits, à faible coût ;
- l'hypothèse
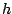 obtenue est Probablement Approximativement
Correcte (d'où; le nom du modèle PAC) ;
obtenue est Probablement Approximativement
Correcte (d'où; le nom du modèle PAC) ;
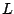 doit fonctionner quelle que soit la distribution des
exemples ; cela dit,
doit fonctionner quelle que soit la distribution des
exemples ; cela dit, 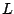 perçoit cette
distribution à travers l'oracle ;
perçoit cette
distribution à travers l'oracle ;
En général, on ajoute une notion d'efficacité : 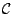 est dite efficacement PAC-apprenable si en plus des conditions précédentes,
est dite efficacement PAC-apprenable si en plus des conditions précédentes,
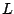 est polynmial en
est polynmial en
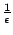 et
et 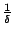 .
.
Une application
On va montrer ici que la classe des rectangles de 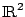 parallèles aux axes
est efficacement PAC-apprenable.
parallèles aux axes
est efficacement PAC-apprenable.
Proposition pour l'apprenant 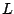 :
:
- constituer un échantillon
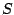 en tirant
en tirant 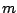 exemples à l'aide de l'oracle ;
exemples à l'aide de l'oracle ;
- construire
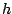 comme le plus petit rectangle contenant tous les exemples positifs de
comme le plus petit rectangle contenant tous les exemples positifs de 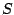 ;
;
- retourner
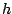 .
.
Il faut maintenant prouver que pour 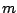 bien choisi et quels que soient le concept cible
bien choisi et quels que soient le concept cible 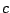 ,
la distribution
,
la distribution 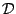 et les paramètres
et les paramètres 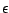 et
et 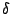 ,
, 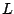 fournit une hypothèse
fournit une hypothèse 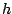 qui
vérifie
qui
vérifie 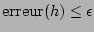 avec une probabilité
avec une probabilité 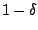 .
.
Intuitivement, plus 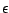 et
et 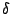 sont petits, plus le
sont petits, plus le 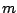 requis doit être grand. Il
faudra vérifier que
requis doit être grand. Il
faudra vérifier que 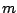 s'exprime comme un polynôme de
s'exprime comme un polynôme de
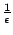 et
et
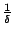 .
.
... à suivre...
Notion d'apprenabilité faible
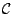 est faiblement PAC-apprenable s'il existe un algorithme
est faiblement PAC-apprenable s'il existe un algorithme 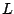 tel que
tel que
- pour
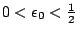 fixé,
fixé,
- pour
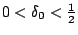 fixé,
fixé,
- pour tout concept
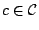 ,
,
- pour toute distribution
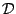 sur
sur 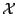 ,
,
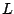 fournit une hypothèse
fournit une hypothèse 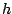 de
de 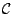 qui, avec une probabilité
qui, avec une probabilité 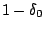 , vérifie :
, vérifie :

Dans cette définition, on demande simplement que les hypothèses produites soient meilleures qu'un étiquetage purement aléaroire.
De manière assez inattendue, il a été prouvé que les deux notions d'apprenabilité sont équivalentes. Cela signifie que, dans le cadre PAC, un apprenant faible (un peu meilleur que l'aléatoire) peut être transformé en un apprenant fort (avec une erreur aussi proche de 0 que voulu), et ce en temps polynomial. Les preuves de ce résultat reposent sur la définition d'un apprenant fort opérant le boosting d'un apprenant faible.
Exercices
Lectures
Learnability and the Vapnik-Chervonenkis dimension
Journal of the ACM, 36(4):929--965, 1989.
[ version pdf ]
Equivalence of Models for Polynomial Learnability
Information and Computation 95(2): 129-161, 1991.
[ version pdf ]
